OpenJDK JEP 180: HashMap, collisions & attaques par la complexité

Cette dépêche parle de la JEP 180 d'OpenJDK 8 qui propose une solution intéressante aux problèmes d'attaques sur la complexité que rencontrent les tables de hachage.

On a déjà parlé de ce sujet ici même à plusieurs reprises. Je vais cependant rapidement représenter le problème et l'évolution des discussions. Le lecteur averti sur le sujet ira directement au dernier paragraphe pour voir la proposition de la JEP 180.

NdM : merci à ckyl pour son journal.

Sommaire

• Présentation des tables de hachage
• Attaques par la complexité
• Java 7u6 & « alternative string-hashing »
• Attaques par la complexité (bis)
• JEP 180: Une solution intéressante
  • Conclusion

Présentation des tables de hachage

Une table de hachage est une implémentation du type abstrait tableau associatif. Un tableau associatif permet d'associer une clé à une ou plusieurs valeurs, on le nomme aussi parfois dictionnaire. Il fait partie des types abstraits les plus utilisés avec les listes.

Une table de hachage est une implémentation particulière d'un tableau associatif. Elle est aussi la plus courante. Basiquement il s'agit d'un tableau dont les cases contiennent un pointeur vers nil, un élément ou une liste d'élément. On détermine la case à utiliser en appliquant une fonction de hachage à la clé. Idéalement, chaque case ne pointera que vers un unique élément. Dans ce cas les opérations d'insertion, de consultation et de suppression se font en temps constant, noté , c'est à dire qui ne dépend pas du nombre d'éléments présents dans la table de hachage. Cependant si la fonction de hachage retourne deux fois la même valeur pour deux clés différentes, ce que l'on nomme collision, alors les deux valeurs sont généralement stockées comme une liste. C'est à dire que maintenant il va falloir parcourir toute cette liste. Dans le pire cas, la fonction de hachage retourne toujours la même valeur, toutes les valeurs vont donc être stockées dans la même case et l'on va devoir parcourir la liste pour chaque opération. La complexité est alors linéaire par rapport au nombre d'éléments dans la structure, noté , ce qui est très peu performant. Une table de hachage a donc une complexité moyenne d' mais un pire cas en . Il est donc crucial d'avoir une fonction de hachage performante. Les personnes n'étant pas à l'aise avec l'implémentation d'une table de hachage ou les concepts précédant auront tout intérêt à consulter la page Wikipédia qui est assez complète.

Cet article s'accompagne d'un benchmark écrit avec JMH qui va nous permettre d'observer comment se comporte la classe HashMap de Java dans différentes circonstances. Le code de ce benchmark est extrêmement simple:

  @GenerateMicroBenchmark
  public int put() {
    HashMap<String, Object> map = new HashMap<String, Object>();

    for (String s: strings) {
      map.put(s, s);
    }

    return map.size();
  }

Nous insérons une collection de chaîne de caractère dans une HashMap et nous mesurons le temps moyen de cette opération. Mesurer l'insertion est une métrique correcte pour ce que nous souhaitons mesurer car lors d'une insertion, dans le cas où la clé existe déjà il faut remplacer la valeur existante. Il faut donc rechercher parmi toutes les clés déjà existantes dans cette case. Les comportements en consultation et en suppressions seront similaires à celui que nous observons. Dans tous les cas, en cas de collision, il faudra traverser toutes les valeurs de cette case. Exemple du code de la méthode put():

    public V put(K key, V value) {
        if (key == null)
            return putForNullKey(value);
        int hash = hash(key.hashCode());
        int i = indexFor(hash, table.length);
        for (Entry<K,V> e = table[i]; e != null; e = e.next) {
            Object k;
            if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
                V oldValue = e.value;
                e.value = value;
                e.recordAccess(this);
                return oldValue;
            }
        }

        modCount++;
        addEntry(hash, key, value, i);
        return null;
    }

On peut clairement y voir les étapes suivantes:

• On calcule le hash de la clé, qui va déterminer la case i
• On itère sur toutes les clés présentes dans la case i pour regarder si une correspond à key
  • Si oui, alors on remplace la valeur existante par value
  • Sinon, on ajoute un nouvel élément pour cette clé à la fin de la liste

Comme on le voit avec la ligne suivante int hash = hash(key.hashCode());, en Java la case est calculée à partir de la valeur retournée par hashCode(). On applique en plus la fonction hash() afin d'améliorer un peu la distribution des clés. En effet, i est calculé modulo la taille de la table qui est une puissance de deux, et il est facile d'avoir des effets néfastes:

   /**
     * Applies a supplemental hash function to a given hashCode, which
     * defends against poor quality hash functions.  This is critical
     * because HashMap uses power-of-two length hash tables, that
     * otherwise encounter collisions for hashCodes that do not differ
     * in lower bits. Note: Null keys always map to hash 0, thus index 0.
     */
    static int hash(int h) {
        // This function ensures that hashCodes that differ only by
        // constant multiples at each bit position have a bounded
        // number of collisions (approximately 8 at default load factor).
        h ^= (h >>> 20) ^ (h >>> 12);
        return h ^ (h >>> 7) ^ (h >>> 4);
    }

Enfin le cas qui va nous intéresser particulièrement ici est celui des chaines de caractères comme clé car c'est une utilisation extrêmement courante et exposée aux attaques. Souvent les données fournies par l'utilisateur sont des chaînes de caractères plutôt que des objets complexes. Par exemple les en-tête HTTP sont souvent stockés dans un tableau associatif.

Regardons donc comment est implémenté le hashCode de la classe String:

   /**
     * Returns a hash code for this string. The hash code for a
     * <code>String</code> object is computed as
     * <blockquote><pre>
     * s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
     * </pre></blockquote>
     * using <code>int</code> arithmetic, where <code>s[i]</code> is the
     * <i>i</i>th character of the string, <code>n</code> is the length of
     * the string, and <code>^</code> indicates exponentiation.
     * (The hash value of the empty string is zero.)
     *
     * @return  a hash code value for this object.
     */
    public int hashCode() {
        int h = hash;
        int len = count;
        if (h == 0 && len > 0) {
            int off = offset;
            char val[] = value;

            for (int i = 0; i < len; i++) {
                h = 31*h + val[off++];
            }
            hash = h;
        }
        return h;
    }

Cela correspond à une fonction de hachage non cryptographique très courante pour les chaînes de caractères. C'est une variante du Bernstein hash, aussi appelé djb2. Elle a ceci d'intéressant qu'elle est utilisée par beaucoup de plateformes et qu'expliquer pourquoi elle marche et comment et pourquoi ont été choisies les valeurs est assez difficile. Les gens intéressés pourront découvrir d'autres fonctions ainsi que passer beaucoup de temps à chercher les réponses à la question précédente.

Dans tous les cas nous appellerons cette variante de dbj2 sous le doux nom de DJBX31A.

Maintenant exécutons notre benchmark en utilisant Java 6u45 avec des chaines aléatoires de taille constante, 15 caractères, pour des collections allant de 10 à 30.000 éléments. Le résultat est le suivant:

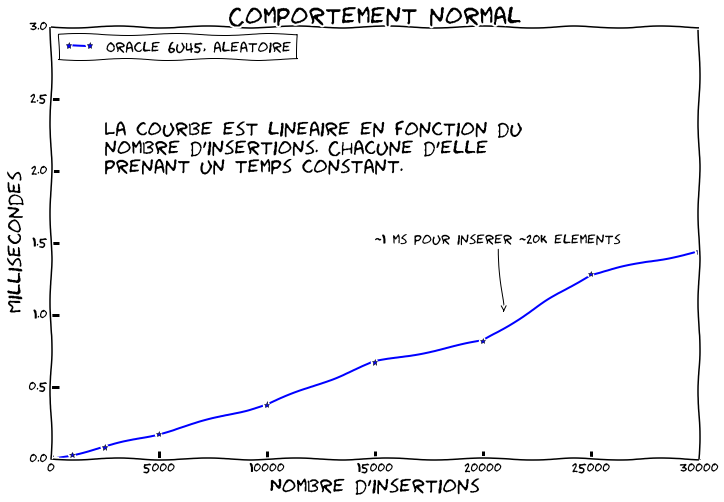
Dans ce cas nous avons le comportement normal attendu. Il y a peu de collisions. En moyenne le temps d'insertion est constant et ne dépend pas de la taille de la collection, . Nous voyons donc que la courbe est linéaire puisque nous répétons fois une opération prenant un temps donné. Nous voyons aussi que nous arrivons à insérer environ 20 000 éléments par milliseconde.

Attaques par la complexité

Si vous avez bien suivi la première partie, vous savez que la performance d'une table de hachage dépend du nombre de collisions et donc de la qualité de sa fonction de hachage. Par nature une table de hachage ne permet pas de garantir que les opérations seront en , il s'agit seulement du cas moyen quand tout se passe bien. La performance au pire cas est .

Ce fait est connu de tout étudiant ayant suivi une introduction à l'algorithmique. Seulement il y a quelques années certains ont eu l'idée d'utiliser ce pire cas pour faire des dénis de service. C'est une attaque par la complexité. L'idée est simple, beaucoup d'applications stockent en mémoire des chaînes de caractères fournies par un utilisateur dans une table de hachage. S'il arrive à fournir des chaînes qui vont systématiquement créer des collisions, alors il va pouvoir ralentir très fortement le système.

L'idée n'est pas nouvelle, elle a été parfaitement documentée en 2003 par Scott A. Crosby et Dan S. Wallach lors de l'Usenix-Sec. Ils avaient alors étudié Perl, qui avait réagi et fourni un correctif. Tout le monde a alors oublié cette histoire pendant quelques années.

En 2011, Alexander Klink et Julian Wälde se souviennent de cette histoire et partent alors explorer ce qu'il est possible de faire avec presque 10 ans après. Les slides du 28C3 décrivent très bien ce qu'ils trouvent. En gros presque toutes les plateformes majeures sont vulnérables de PHP à Java en passant par Python puisque tout le monde ou presque utilise une variante de djb2, pour lequel il est très facile de générer des collisions. Le résultat c'est qu'on peut faire un déni de service sur à peu près n'importe quoi avec très peu de données. Avec 2 MB de données ils arrivent à occuper un processeur pendant plus d'une demi-heure.

Le benchmark suivant compare la courbe précédente avec une où toutes les clés se retrouvent dans la même case car on génère spécialement les clés pour que DJBX31A retourne toujours la même valeur bien que les chaînes soient différentes.

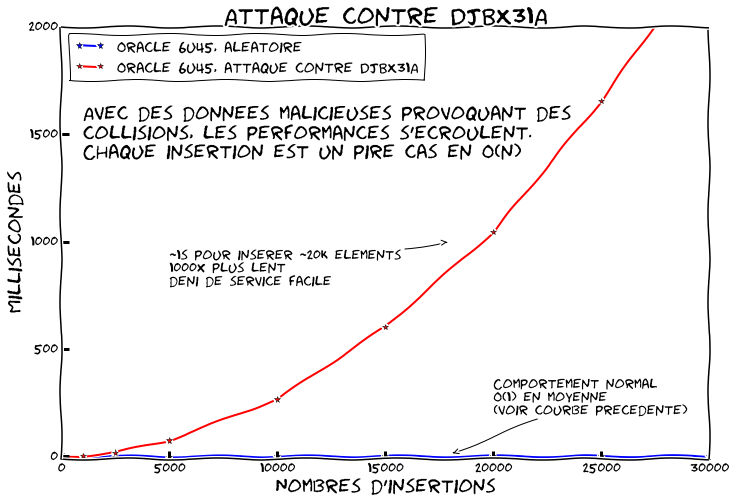
Comme on peut le voir l'effet est plutôt dramatique. Chaque insertion dépend donc maintenant du nombre d'éléments dans la table de hachage. Si vous vous rappelez du code de la méthode put(), nous avons à parcourir tous les éléments à chaque fois. Puisque nous allons insérer un nouvel élément, il faut vérifier tous les autres. La courbe devient donc quadratique. Pour 20 000 éléments on peut voir que l'on est déjà 1000 fois plus lent. Vous pouvez facilement extrapoler pour 50 000 ou 100 000.

Java 7u6 & « alternative string-hashing »

Comme la plupart des plateformes impactées par cette découverte, Java cherche une solution. Et beaucoup vont choisir une solution similaire. L'idée est qu'il faut empêcher un utilisateur de pouvoir générer des collisions. Une solution est d'utiliser des fonctions de hachage cryptographiques qui sont conçues pour cela. En pratique ce n'est pas possible car elles sont beaucoup trop lentes (grossièrement il y a au minimum un ordre de grandeur d'écart). Le consensus est alors de migrer vers une autre fonction de hachage: Murmur 2 ou 3. Murmur est une bonne fonction de hachage non cryptographique, elle est rapide et fournit de bons résultats. En plus on peut l'initialiser avec une graine qui va conditionner la valeur de sortie. L'idée est donc de générer la graine à l'exécution. Il devient alors compliqué pour l'utilisateur de générer des collisions car il a besoin de la graine et qu'il n'y a pas accès.

Python utilise cette solution et décide de changer sa fonction de hachage pour Murmur.

Java veut faire de même mais a un problème supplémentaire. La Javadoc de la méthode hashCode de String documente l'implémentation sous-jacente:

 /**
     * Returns a hash code for this string. The hash code for a
     * <code>String</code> object is computed as
     * <blockquote><pre>
     * s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
     * </pre></blockquote>
     * using <code>int</code> arithmetic, where <code>s[i]</code> is the
     * <i>i</i>th character of the string, <code>n</code> is the length of
     * the string, and <code>^</code> indicates exponentiation.
     * (The hash value of the empty string is zero.)
     *
     * @return  a hash code value for this object.
     */

DJBX31A fait donc partie du contrat de la classe, et on ne peut pas le changer sans risque de casser la compatibilité et le comportement des applications. C'est une règle stricte du côté de Java.

Pour cette raison on imagine donc ce qui est pour moi l'un des patchs les plus dégueulasses de l'histoire du JDK qui a été livré en Java 7u6. En gros on ne touche à rien de ce qui existe. On rajoute une nouvelle méthode hash32 à la classe String qui repose sur Murmur.

   int hash32() {
        int h = hash32;
        if (0 == h) {
           // harmless data race on hash32 here.
           h = sun.misc.Hashing.murmur3_32(HASHING_SEED, value, 0,
value.length);

           // ensure result is not zero to avoid recalcing
           h = (0 != h) ? h : 1;

           hash32 = h;
        }

        return h;
    }

Maintenant on patche les collections utilisant des fonctions de hachage pour faire la chose suivante : on regarde le type de l'élément, si c'est String alors on invoque hash32 par une introspection dédiée car la méthode n'est pas publique, sinon on invoque hashCode. Seulement les String sont immutables, et la valeur de hashCode était cachée pour éviter de la recalculer à chaque fois. On doit donc faire de même avec hash32 qui impose donc 4 octets supplémentaire à chaque instance de String. Pour finir on initialise HASHING_SEED dynamiquement à l'initialisation pour empêcher les collisions.

C'est cool on n'a pas touché à hashCode ! Seulement voilà le comportement des applications peut toujours changer même en remplaçant la fonction de hachage uniquement dans les collections. Alors on rajoute un flag pour décider si on veut oui ou non utiliser le alternative string-hash dans les collections.

Voir le courriel sur la liste de discussion d'OpenJDK ainsi que le patch.

Voilà ça pique les yeux mais ça fait le job ! Refaisons tourner le même benchmark avec Java 7u55:

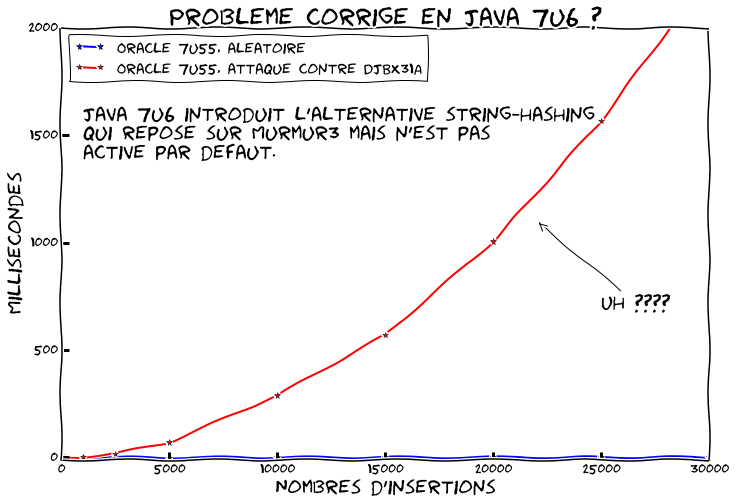
Ah oui j'ai dit qu'il y avait une option pour l'alternative string-hashing mais j'ai pas dit qu'elle était activée par défaut… Recommençons avec -Djdk.map.althashing.threshold=1

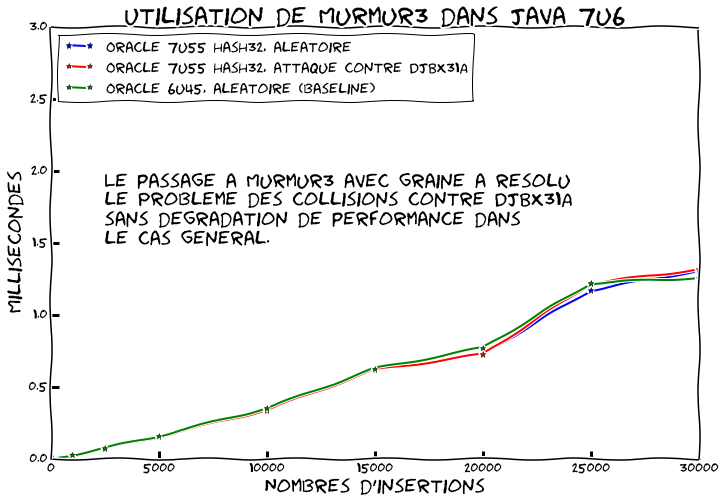
C'est mieux non ? Bon OK par défaut on est toujours vulnérable trois ans après…

Attaques par la complexité (bis)

Seulement voilà, entre temps quelques-uns ont commencé à creuser le problème. Ils ont attaqué Murmur3 avec graine qui n'a pas tenu très longtemps. Ca a d'ailleurs été présenté au 29c3. Dans les speakers on notera DJB, oui c'est le même.

Rebelote, tous ceux qui sont passés à Murmur sont impactés ainsi que quelques copains dont les fonctions ont aussi été cassées. C'est un peu moins trivial de générer des collisions avec Murmur mais le travail difficile a été fait pour nous. On n'a qu'à écrire le code…

Essayons de refaire tourner notre benchmark en générant des collisions contre Murmur:

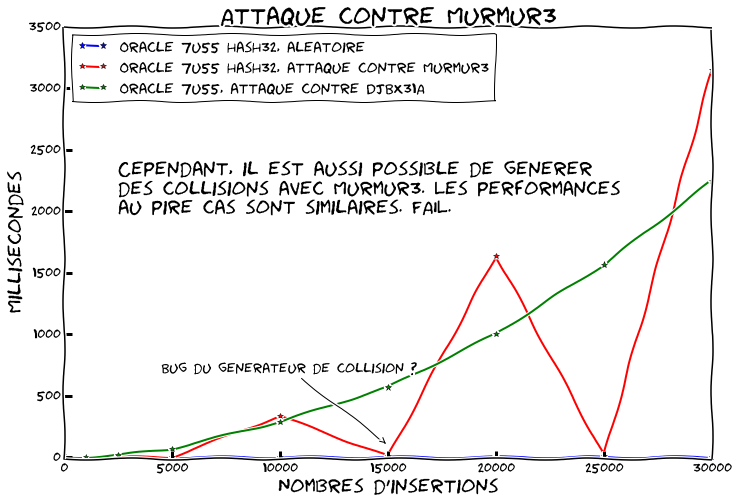
Cette fois nous comparons le comportement usuel avec:

• Des collisions contre DJBX31A sans l'alternative string-hashing
• Des collisions contre Murmur3 avec l'alternative string-hashing

(Je n'ai pas investigué les deux points à 15k et 25k qui sont très étranges. Le générateur passe les tests unitaires et les résultats eux sont stables…)

C'est grosso modo la même chose. On a donc fait un patch moche qui ne sert plus à rien puisque dans les deux cas on est vulnérable…

JEP 180: Une solution intéressante

Maintenant qu'est-ce qu'on fait ?

En même temps qu'ils ont cassé Murmur avec graine, DJB et ses potes ont proposé une nouvelle fonction de hachage: SipHash. Elle est vendue comme étant aussi rapide que les précédentes mais résistante aux attaques par collisions.

La plupart des plateformes ont migré vers SipHash, Python par exemple. Et comme on s'est déjà fait avoir une fois on en profite pour faire la PEP 456 qui permet d'avoir des fonctions de hash interchangeable pour les chaîne de caractères et tableaux d'octets. On bascule à SipHash mais comme on sait que ça risque de recommencer, on prévoit le coup…

Du côté de Java on a toujours le même problème avec hashCode, rechanger hash32 fait prendre quelques risques aussi et le patch initial étant "crado" on aimerait bien s'en débarrasser. On choisit donc une approche radicalement différente. Plutôt que de chercher une fonction de hachage parfaite, on rebascule sur DJBX31A. On s'applique plutôt à résoudre le problème du au pire cas. Le vient du fait que les collisions sont gérées avec une liste chaînée. Si on utilise un arbre balancé plutôt qu'une liste on passe en ce qui réduit drastiquement le problème.

C'est ce que propose la JEP 180 et qui a été implémenté dans OpenJDK 8.

Refaisons tourner notre benchmark sur OpenJDK 8:

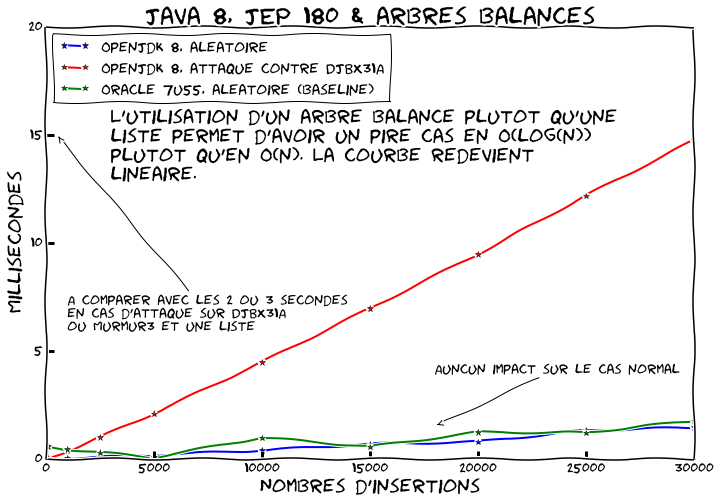
Cette fois ci nous comparons le comportement normal d'OpenJDK 8 et Java 7u55 ainsi que le comportement d'OpenJDK8 avec des collisions.

Tout d'abord nous constatons que les performances dans le cas normal n'ont pas régressé. Ensuite nous voyons que contrairement à une solution qui vise a prévenir entièrement les collisions, l'utilisation d'arbre balancé a tout de même un coût. Les opérations passent de à . Cependant si on regarde les chiffres ce n'est pas dramatique. À 20 000 éléments nous sommes maintenant à ~10ms plutôt que ~1ms loin de la seconde initiale.

Nous avons regardé le point de vue performance, cependant utiliser des arbres balancés a aussi un impact non négligeable sur la consommation mémoire. En effet au lieu d'avoir à stocker un bête pointeur sur l'élément suivant, on se retrouve avec quatre pointeurs et un booléen. Ce qui pourrait faire exploser la consommation mémoire. Cependant par défaut on utilise toujours une liste chaînée. Quand le nombre de collisions augmente dans une case et dépasse un seuil on convertit tout ou une partie de la liste en arbre balancé pour optimiser le ratio consommation mémoire/performance. Cette technique est appliquée à chaque feuille de l'arbre. On démarre avec une liste, puis on convertit la feuille en arbre quand elle devient trop grande. Quand on supprime des éléments on peut rebasculer vers une liste chaînée. Les seuils de conversion étant respectivement à 8 et 6 éléments.

Si l'on observe la consommation mémoire avec Jol on peut voir que ça marche très bien:

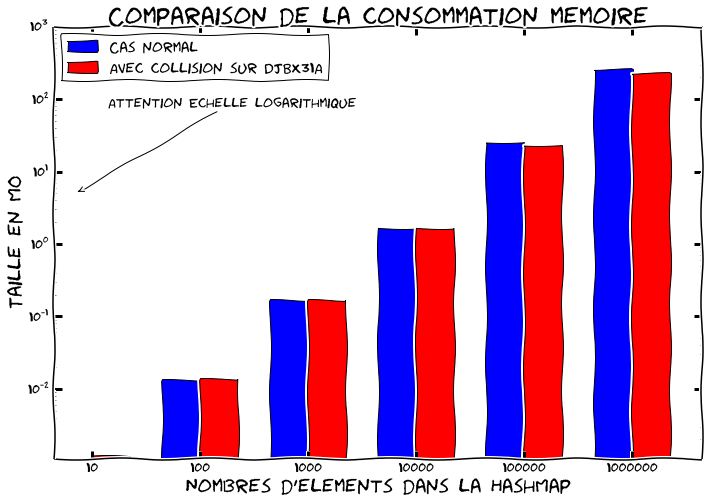
Ici on a fait attention à ce que les chaînes aient toujours la même taille dans les deux cas.

En pratique dans une utilisation courante avec une fonction de hachage correcte, les collisions seront rares et les arbres balancés ne seront jamais utilisés. Par contre quand ils rentrent en action cela permet d'éviter les DOS ou simplement d'avoir de bonnes performances quand la fonction hashCode de l'utilisateur est biaisée.

J'invite le lecteur intéressé à aller regarder le code. Le commentaire initial explique extrêmement clairement comment ça fonctionne et c'est plutôt rigolo à lire.

Conclusion

L'approche d'OpenJDK 8 est intéressante et différente des autres plateformes puisqu'elle ne cherche pas à résoudre le problème des collisions mais à améliorer le pire cas. Changer de fonction de hachage pour les String étant compliqué on peut comprendre ce choix. Ils ont fait le pari que les performances offertes par les arbres balancés suffiront à se protéger et à offrir une bonne robustesse aux mauvaises fonctions de hachage. En pratique, au pire cas on observe un ralentissement constant de ~10x quelle que soit la taille de la collection.

De l'autre côté beaucoup de plateformes ont changé de fonction de hachage pour éviter le pire cas mais n'ont pas cherché à l'améliorer et sont restés aux listes chainées. Ils se protègent donc des dénis de service selon les connaissances actuelles mais ne cherchent pas à se protéger pour le futur ni à offrir une réponse performante aux fonctions de hachage qui pourraient être légèrement biaisées pour certains autres types de données car implémentées par l'utilisateur.

Dans l'idéal les deux techniques devraient être appliquées mais je ne connais pas de plateforme qui le fasse. Et vous les outils que vous utilisez ils ont fait quoi ?

Voilà c'est un problème pas nouveau mais on en entendra certainement à nouveau parler. Dès qu'on lit une valeur du monde extérieur, celui-ci va s'arranger pour trouver un moyen de faire des choses "sympas". Les attaques algorithmiques permettent de varier un peu les plaisirs et forcent à s'interroger longuement à chaque fois qu'on stock une valeur que l'on ne contrôle pas.

Note: Tout le matériel créé pour écrire l'article est en ligne.

NdM : Pour ceux qui se demandent comment sont fait les graphiques, ils s'agit du mode xkcd de matplotlib comme expliqué par l'auteur dans les commentaires du journal à l'origine de la dépêche.

Aller plus loin

• Journal à l'origine de la dépêche (85 clics)
• Dépêche précédente sur la JEP 142 (36 clics)