Journal résoudre "trouve 24"

Posté par steph1978 le 23 février 2022 à 12:57. Licence CC By‑SA.

Étiquettes :

fév.

2022

Wordle est mort. Racheté par le capitalisme et blindé de tackers et de pubs.

Changeons de jeu : trouver 24.

Le but est de combiner les 4 nombres proposés en 3 opérations pour atteindre le nombre 24.

Un petit exemple : 8 5 7 1 sortent, on peut faire 8-5=3, 7+1=8, 3*8=24.

Il est obligatoire d'utiliser tous les nombres. Par exemple : 1 2 3 8 sortent, on ne peut pas faire 8 * 3 = 24, car 1 et 2 n'ont pas été utilisés.

J'ai joué un peu puis me suis dis "c'est un boulot pour une machine".

Le jeu resemble un peu au jeu le compte est bon, avec 4 nombres au lieu de 6 et trouver 24 au lieu d'un nombre entre 101 et 999 et le fait qu'il faut utiliser tous les nombres.

J'ai donc ressorti un code que j'ai écrit en 1999 (oui monsieur!), en C et qui résolvait "le compte est bon" en une fraction de seconde sur un processeur PPC G3 de 233MHz.

Le programme est brute force. Il tente toutes les combinaisons possibles (733'188 si mon dénombrement est le bon) avec un parcours récursif systématique. Il ne tente pas de réutiliser les résultat précédents. Par exemple quand on calcule les combinaisons pour (a1,a2,a3,a4,a6), une grosse partie - (a1,a2a3,a4) - a déjà été exploré quand on a fait (a1,a2,a3,a4,a5). Mais mettre en place de la mémorisation m'a paru bien plus compliqué que le brute force.

Le code est probablement très laid pour un pratiquant du C. Ce n'est pas mon cas. Et deux décennies après, j'ai pu m'y replonger et l'adapter sans problème. Je n'ai pas eu trop honte de mon ancien moi à la relecture :)

$ ./trouve_24 1 2 3 8 
1 + 2 = 3 ; 3 * 8 = 24 ;  
1 + 2 = 3 ; 8 * 3 = 24 ;  
1 * 2 = 2 ; 3 * 8 = 24 ;  
1 - 2 = 1 ; 3 * 8 = 24 ;  
1 - 2 = 1 ; 8 * 1 = 8 ; 3 * 8 = 24 ;  
1 + 3 = 4 ; 2 - 8 = 6 ; 4 * 6 = 24 ;  
1 + 3 = 4 ; 8 + 4 = 12 ; 2 * 12 = 24 ;  
1 * 3 = 3 ; 8 * 3 = 24 ;  
1 + 8 = 9 ; 3 + 9 = 12 ; 2 * 12 = 24 ;  
1 * 8 = 8 ; 3 * 8 = 24 ;  
2 - 8 = 6 ; 1 + 3 = 4 ; 6 * 4 = 24 ;  
3 + 8 = 11 ; 1 + 11 = 12 ; 2 * 12 = 24 ;  
3 * 8 = 24 ;  
420 numbers generated 
13 solutions

À noter que le programme donne des solutions invalides qui n'utilisent pas tous les nombres, il faut filtrer. Je n'ai pas non plus implémenté la division qui me paraissait plus compliquée qu'utile à l'époque pour le compte est bon. Pour trouve 24, il peut être nécessaire de l'utiliser pour consommer des nombres. Dans ce cas, le programme ne donne pas de solution et il faut donc se dire qu'une division est nécessaire. Cela réduit alors le problème qui devient facilement résoluble de tête.

Est-ce que vous avez déjà tenté de résoudre ce type de puzzle ? Si oui quelle a été votre approche ?

Ah et si les chiffres c'est pas votre truc, mais que vous aimez la géographie, découvrez worldle, avec ou sans openstreetmap sous les yeux, c'est pas le même délire.

# Quelques pensées

Posté par 🚲 Tanguy Ortolo (site web personnel) le 23 février 2022 à 13:53. Évalué à 5.
Si je ne m'abuse, les résultats intermédiaires se ramènent à une utilisation de parenthèses, et en somme, une solution possible a forcément la forme d'un arbre binaire, les opérations utilisées ayant à chaque fois deux termes. Même si plusieurs arbres peuvent être équivalent à cause de la commutativité de l'addition et de la multiplication.

Bref, des arbres binaires avec quatre feuilles, il n'y en a pas trente-six, en fait il n'y en a que deux si je ne m'abuse, les autres formes possibles étant équivalentes à celles-ci en échangeant des nombres :
```
 /\          /\
a /\        /  \
 b /\      /    \
  c  d    /\    /\
         a  b  c  d
```
Donc, deux formes d'arbres, 4! répartitions des quatre nombres, et, les arbres ayant 3 nœuds sur lesquels il faut choisir à chaque fois une opération parmi les quatre opérations de base, 4³ choix d'opérations. Soit un total de 3072 possibilités. Je me trompe ?

On pourrait envisager d'optimiser le calcul en réutilisant des résultats de sous-arbres. Cela implique d'utiliser une forme de cache, et je ne suis en fait pas certain que ce soit vraiment plus efficace que de calculer sans cache. Un avis ?
- [^] # Re: Quelques pensées
  
  Posté par 🚲 Tanguy Ortolo (site web personnel) le 23 février 2022 à 14:32. Évalué à 4.
  
  Quoi que, connaissant d'avance la forme des arbres, on peut procéder à l'inverse, du bas vers le haut, et calculer toutes les possibilités de couples, puis les assembler.
- [^] # Re: Quelques pensées
  
  Posté par steph1978 le 23 février 2022 à 17:37. Évalué à 2.
  
  Soit un total de 3072 possibilités. Je me trompe ?
  
  Quand on fait "échouer" le programme - par exemple ./trouve_24 1 1 1 1 ne parviendra pas à trouver de solution - le programme annonce avoir tester 543 combinaisons. Il a parcourus tout l'espace de recherche, pas de branches coupées (les break dans le code).
  
  Si je modifie pour avoir 4 opérations (probablement ton calcul), il compte 939 combinaisons.
  
  J'avoue que je n'ai jamais vraiment trouvé le formule qui permet de calculer le nombre de combinaisons, encore une fois j'ai fait la brute en les comptant une par une :)
  
  J'étais arrivé à ça mais je ne sais plus comment et je ne retombe pas sur les chiffres donnés par le programme.
  
  Après, ça reste une jolie formule :D
  
  On pourrait envisager d'optimiser le calcul en réutilisant des résultats de sous-arbres.
  
  On peut mesurer que le programme utilise vraiment peu de mémoire (on pourrait faire un calcul théorique).
  
  Pour un espace de recherche aussi petit, je ne pense pas qu'une stratégie de cache soit efficace.
  
  Cependant, j'y vois un intérêt théorique :) : J'aimerai voir un programme qui minimise le nombre de calcul en réutilisant les sous-résultats. J'avais essayé pour 'le compte est bon' car l'espace de recherche est plus grand (733'188 si mon dénombrement est le bon) et que mon CPU était beaucoup plus faible. Mais j'ai laissé tombé devant la complexité et le fait que la méthode brute force donnait un résultat très rapidement.
  - [^] # Re: Quelques pensées
    
    Posté par steph1978 le 23 février 2022 à 20:06. Évalué à 2.
    
    Alors, si mes calculs sont bon, j'ai une erreur dans ma formule et un gros bug dans le comptage dans mon programme.
    
    La formule serait :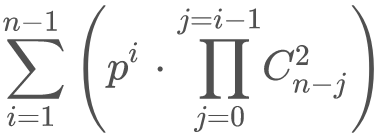
    
    Remarquez la division par deux qui a disparue. Elle était la pour la commutativité. Mais en fait c'est déjà pris en compte par l'opération "combinaison" C(n-j,2) qui n'a pas de notion d'ordre - (a,b) est (b,a) sont comptés pour 1.
    
    J'ai un alignement des planètes : pour "trouve 24" - 4 nombres et 4 opérateurs - on aurait 1464 combinaisons (en comptant aussi celle de 1 ou 2 opérations qui ne sont pas valides). Pour "le compte est bon" - 6 nombres et 3 opérateurs - on aurait 900'495 combinaisons.
    
    Si qqun savait confirmer les chiffres, ça serait top.
# En Prolog

Posté par Blackknight (site web personnel, Mastodon) le 23 février 2022 à 14:56. Évalué à 6.

En voyant le type de problème et vu ma tendance à aimer les vieux langages (est-il besoin de le préciser), j'ai tout de suite pensé à Prolog.

Forcément, il y a déjà quelqu'un qui a codé une solution(Tout en bas de cette page) :)

Bon, ce n'est pas forcément très simple à comprendre quand on ne connait pas le langage et même quand on connait, il faut se creuser pour tout assimiler mais c'est sympa pour s'ouvrir un peu les chakras.
- [^] # Re: En Prolog
  
  Posté par zurvan le 24 février 2022 à 19:38. Évalué à 3.
  
  faut que je me remette à Prolog ! J'en ai fait à la fac (de lettres), c'était pour programmer des pluriels et autres déclinaisons dans différentes langues, j'avais trouvé ça passionnant…
  
  ce programme est bien fichu, par contre il ne va pas forcément utiliser tous les nombres proposés, ce qui est demandé par le jeu 24. Je serai incapable de modifier le programme prolog pour prendre ça en compte, mais ça doit être trivial pour qui connait ce langage :)
  
  « Le pouvoir des Tripodes dépendait de la résignation des hommes à l'esclavage. » -- John Christopher
  - [^] # Re: En Prolog
    
    Posté par Blackknight (site web personnel, Mastodon) le 25 février 2022 à 09:31. Évalué à 3.
    
    Voilà un défi intéressant pour s'y remettre :)
    Je vais essayer de plancher dessus, c'est inutile donc indispensable.
    - [^] # Re: En Prolog
      
      Posté par Blackknight (site web personnel, Mastodon) le 28 février 2022 à 18:45. Évalué à 5.
      Bon, j'ai eu un peu de temps pour adapter le code trouvé sur l'autre jour et voici la solution en Prolog:
      
      bonCompte(N, [N],[]):-!. bonCompte(N, L,[Detail|Details]):- choisir2elements(Op1, Op2, Reste, L), calcul(Resultat, Op1, Op2, Detail), bonCompte(N, [Resultat|Reste],Details). choisir2elements(Operande1, Operande2, Reste, Liste):- select(Operande1, Liste, Reste1), select(Operande2, Reste1, Reste), Operande1 >= Operande2. calcul(Res, Op1, Op2, [Op1, '+', Op2, '=', Res]):- Res is Op1 + Op2. calcul(Res, Op1, Op2, [Op1, '*', Op2, '=', Res]):- Op2 >= 1, Res is Op1 * Op2. calcul(Res, Op1, Op2, [Op1, '-', Op2, '=', Res]):- Res is Op1 - Op2, Res > 0. calcul(Res, Op1, Op2, [Op1, '/', Op2, '=', Res]):- Op2 >= 1, Res is Op1 / Op2, integer(Res), Res \== Op2.
      
      Le second paramètre de bonCompte étant une liste contenait en tête le résultat, il suffisait de vérifier que cette liste ne contenait que le résultat. C'est ce que dit la première règle.
      
      J'ai autorisé le fait que le résultat de la soustraction puisse fournir la même chose que sa opérande (le cas 2-1=1) et autorisé qu'une division et une multiplication par 1 soit faisable.
      
      Ca s'appelle simplement via bonCompte(24, [7,8,5,1]). par exemple
      - [^] # Re: En Prolog
        
        Posté par Gil Cot ✔ (site web personnel, Mastodon) le 01 mars 2022 à 01:52. Évalué à 3. Dernière modification le 01 mars 2022 à 01:52.
        
        Juste excellent ! Je n'ai pas eu le temps dimanche (je comptais jeter un œil pour dérouiller mon Prolog —découverte d'adolescence que j'avais beaucoup aimé)
        
        “It is seldom that liberty of any kind is lost all at once.” ― David Hume
        
        [^] # Re: En Prolog
        
        Posté par Blackknight (site web personnel, Mastodon) le 01 mars 2022 à 10:49. Évalué à 2. Dernière modification le 01 mars 2022 à 10:51.
        
        Par contre, je viens de voir, d'après les commentaires plus bas, que cela ne gère pas les fractions.
        Je pense qu'aux chiffres et aux lettres, on travaille toujours sur des entiers.
        
        Le problème est que je n'ai pas le niveau en Prolog pour corriger cela rapidement.
        
        Peut-être faut-il regarder du côté de rational/1
        
        [^] # Re: En Prolog
        
        Posté par Gil Cot ✔ (site web personnel, Mastodon) le 01 mars 2022 à 12:20. Évalué à 3.
        
        En fait il faudra essayer sur l'exemple problématique : bonCompte(24, [1,4,5,6])
        La solution étant 6/((5/4)-1) ; il ne faudrait pas que s'arrêter à 5/4 qui n'est pas entier, ni même à (5/4)-1 = 1/4 qui n'est pas un entier, donc probablement un truc dans le genre
        
        calcul(Res, Op1, Op2, [Op1, '/', Op2, '=', Res]):- Op2 >= 1, Res is Op1 / Op2, rational(Res).
        
        Ça, ça marcherait aussi pour des cas difficiles du compte est bon. Pour le cas de jeu du Hollandais Volant, d'après le source JS on est plutôt dans du number/1 mais faudrait savoir si on a la même précision de part et d'autre (sachant que les fraction vont couvrir plus de 99% des cas on peut ne pas aller jusqu'à ce niveau de détail.)
        
        Il y a aussi des subtilités avec les soustractions : notre résultat sera forcément positif, mais pas forcément certaines opérations intermédiaires… Par exemple : 1-5=-4; 7-4=3; 3*8=24; avec bonCompte(24, [1,5,3,8]) S'il le trouve pas, faudra probablement modifier
        
        calcul(Res, Op1, Op2, [Op1, '-', Op2, '=', Res]):- Res is Op1 - Op2.
        
        De même, par anticipation, je me demande si les fractions doivent être forcément positives ? (je pense qu'il faudrait utiliser dif au lieu de \= ou \==)
        
        calcul(Res, Op1, Op2, [Op1, '/', Op2, '=', Res]):- Op2 \== 0, Res is Op1 / Op2, rational(Res).
        
        Les tests sur le site web de trouve 24 amènent à changer un peu les bornes qu'on se fixait pour le compte est bon…
        
        “It is seldom that liberty of any kind is lost all at once.” ― David Hume
        
        [^] # Re: En Prolog
        
        Posté par Blackknight (site web personnel, Mastodon) le 02 mars 2022 à 11:41. Évalué à 3.
        
        Il y a aussi des subtilités avec les soustractions : notre résultat sera forcément positif, mais pas forcément certaines opérations intermédiaires… Par exemple : 1-5=-4; 7-4=3; 3*8=24; avec bonCompte(24, [1,5,3,8]) S'il le trouve pas, faudra probablement modifier
        calcul(Res, Op1, Op2, [Op1, '-', Op2, '=', Res]):- Res is Op1 - Op2.
        
        Alors, il faut aussi modifier choisir2elements qui ordonne les deux opérandes sinon on ne passe pas par les négatifs mais dans ce cas, on se récupère tous les doublons liés à la commutativité des opérateurs +, - et *.
        
        Et en plus, pour une raison que j'ignore pour l'instant, cela ne ressort pas ta solution…
        
        On va finir par y arriver à avoir la fédération trouve24 à la TapTempo Federation :D
        
        [^] # Re: En Prolog
        
        Posté par Gil Cot ✔ (site web personnel, Mastodon) le 02 mars 2022 à 12:55. Évalué à 2.
        
        Les doublons : c'est le premier truc qu'on constate :D En général ça se comprend/pardonne sauf quand on a le même chiffre en plusieurs exemplaires en entrée :-/
        
        “It is seldom that liberty of any kind is lost all at once.” ― David Hume
        
        [^] # Re: En Prolog
        
        Posté par Anthony Jaguenaud le 02 mars 2022 à 11:48. Évalué à 3.
        
        (6×4)÷(5-1) et il n’y a que des divisions entières.
        
        [^] # Re: En Prolog
        
        Posté par Gil Cot ✔ (site web personnel, Mastodon) le 02 mars 2022 à 13:06. Évalué à 3.
        
        Il faut que t'ailles sur le site essayer le programme ;) Le code de la page utilise bien des décimaux (ou plus exactement des flottants JS)
        C'est pour éviter les malentendus et voir large qu'on a fini par parler de fractions… ( $\mathbb{N}\subset\mathbb{Z}\subset\mathbb{D}\subset\mathbb{Q}$ )
        
        “It is seldom that liberty of any kind is lost all at once.” ― David Hume
# Mauvais exemple

Posté par groumly le 23 février 2022 à 21:35. Évalué à 10.

on ne peut pas faire 8 * 3 = 24, car 1 et 2 n'ont pas été utilisés.

heu, ben si: 8*3*(2-1) :)
Ok, je chipote.

Linuxfr, le portail francais du logiciel libre et du neo nazisme.
- [^] # Re: Mauvais exemple
  
  Posté par steph1978 le 24 février 2022 à 21:21. Évalué à 3.
  
  Je n'ai pas dit qu'il n'était pas possible de les utiliser - d'ailleurs le site dit "100 % des parties ont une ou plusieurs solutions" - j'ai juste dit qu'il fallait tous les utiliser pour avoir une solution valide.

# un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 24 février 2022 à 03:44. Évalué à 4. Dernière modification le 24 février 2022 à 03:44.

Wordle est mort. Racheté par le capitalisme et blindé de tackers et de pubs.

C'est ballot …parce que, justement dans un lien posté récemment, que l'absence de pisteurs est un des ingrédients du succès.
https://linuxfr.org/users/gilcot/liens/wordle-is-pretty-damn-smart-in-many-subtle-ways

J'ai joué un peu puis me suis dis "c'est un boulot pour une machine".

Ou pas… Ce genre de jeux (le compte est bon) est une façon d'évaluer l'aptitude de calculs mentaux et l'intuition (plutôt la capacité d'estimation) face aux combinaisons de nombres. Évaluer une machine, ou tricher, a peu d'intérêt ici.
Ceci dit, l'informatique y est utile pour évaluer des conjectures mathématiques ou explorer certains aspects algorithmiquement (notamment tout ce qui touche aux arbres de décision, dont il n'est pas question ici puisqu'on emploie la force brute.) Il me semble d'ailleurs avoir vu passer deux articles sur le sujet, dont un dans Tangente si j'ai bonne mémoire.

À noter que le programme donne des solutions invalides qui n'utilisent pas tous les nombres, il faut filtrer. Je n'ai pas non plus implémenté la division qui me paraissait plus compliquée qu'utile à l'époque pour le compte est bon.

Du coup, je vais relever le défi, histoire de me changer les idées après une journée harassante de travail. Et pour épicer un peu la chose, l'implémentation sera en shell POSIX…

Bien, je passe sur l'étape de la saisie des nombres et du contrôle des entrées (toujours.)
Je ne vais pas non plus stocker les solutions, mais plutôt les sortir au fil de l'eau.
Comme on n'a pas de structure de tableau (en KSh, BASh et probablement ZSh, oui) je vais utiliser une variable par nombre (mais il n'y en a heureusement que quatre) !

Mon idée est qu'on va faire une boucle sur la liste de nombres.
Dans un langage comme RPL, on va juste faire quatre tours en décalant…

\<<
  1 4 FOR i
    4 ROLL
    @process
  NEXT
\>>

Pour la plupart des autres langages, non Forth-like on va utilier un tableau et décaler le curseur dans la boucle (tout en prenant tous les éléments, c'est juste pour changer l'ordre à chaque itération.)
Bon, on ne gère pas de tableau et heureusement il n'y a que quatre nombres.

process0 $number1 $number2 $number3 $number4
process0 $number2 $number3 $number4 $number1
process0 $number3 $number4 $number1 $number2
process0 $number4 $number1 $number2 $number3

Ces quatre lignes sont trompeuses (ça m'a servi à valider le fonctionnement, mais) il y a en fait vingt-quatre permutations (prises en compte dans la version finale.)

Le processus va consister à appliquer les quatre opérateurs… de sorte à couvrir tous les cas…
On peut les énumérer, mais par peur d'oublier, je boucle pareillement pour les quatre opérations… (l'optimisation serait de déboucler …parce que sinon on aura des doublons du fait la commutativité, mais cet exercice se fera plus tard.)

process0() {
  for o1 in '+' '-' '*' '/'
  do
    for o2 in '+' '-' '*' '/'
    do
      process1 "$o1" "$o2" "$@"
    done
  done
}

process1() {
  local o1="$1"
  local o2="$2"
  local n1="$3"
  local n2="$4"
  local n3="$5"
  local n4="$6"
  for o3 in '+' '-' '*' '/'
  do
    test $(( (n1 $o1 n2) $o3 (n3 $o2 n4) )) -eq 24 &&
      solution1 "$n1" "$o1" "$n2" "$n3" "$o2" "$n4" "$o3"
  done
}

solution1() {
  local r1=$(( $1 $2 $3 ))
  local r2=$(( $4 $5 $6 ))
  echo "$1$2$3=$r1; $4$5$6=$r2; $r1$7$r2=24"
}

Bon, c'est pas tout ça. Dans ce truc brutalement automatique, il ne faut pas oublier de gérer la division par zéro…

    test "$o1" = '/' && test $n2 -eq 0 && break
    test "$o2" = '/' && test $n4 -eq 0 && break
    test "$o3" = '/' && test "$o2" = '/' && test $n3 -lt $n4 && continue

En plus du second processus, on va appeler un troisième dans la même boucle (c'est du « quick and dirty » et il doit être possible de fusionner les deux…)

process2() {
  local o1="$1"
  local o2="$2"
  local n1="$3"
  local n2="$4"
  local n3="$5"
  local n4="$6"
  test "$o3" = '/' && test $n2 -eq 0 && return
  for o3 in '+' '-' '*' '/'
  do
    test "$o2" = '/' && test "$o3" = '/' && test $n2 -lt $n3 && continue
    test $(( n1 $o1 (n2 $o3 n3) $o2 n4 )) -eq 24 &&
      solution2 "$n1" "$o1" "$n2" "$n3" "$o2" "$n4" "$o3"
  done
}

solution2() {
  local r3=$(( $3 $7 $4 ))
  local r4=$(( $1 $2 $r3 ))
  echo "$3$7$4=$r3; $1$2$r3=$r4; $r4$5$6=24"
}

Enfin, on pense à ajouter les compteurs.

$ trouve24.sh 1 2 3 8
1/2=0; 3*8=24; 0+24=24
1/2=0; 8*3=24; 0+24=24
1+3=4; 8-2=6; 4*6=24
2-1=1; 3*8=24; 1*24=24
2-1=1; 8*3=24; 1*24=24
3+1=4; 8-2=6; 4*6=24
2-1=1; 3*1=3; 3*8=24
2-1=1; 3/1=3; 3*8=24
3*8=24; 1/2=0; 24+0=24
3*8=24; 1/2=0; 24-0=24
3*8=24; 2-1=1; 24*1=24
3*8=24; 2-1=1; 24/1=24
8-2=6; 1+3=4; 6*4=24
2-1=1; 8*1=8; 8*3=24
2-1=1; 8/1=8; 8*3=24
8-2=6; 3+1=4; 6*4=24
8*3=24; 1/2=0; 24+0=24
8*3=24; 1/2=0; 24-0=24
8*3=24; 2-1=1; 24*1=24
8*3=24; 2-1=1; 24/1=24
20 solutions for 2832 computed.

Comme c'est bête/brute et méchant/truand, il m'annonce vingt réponses qui pourraient se ramener à 10 du fait des symétries et on a exploré deux mille huit cents combinaisons dont on aurait pu se passer du quart je pense.
J'ai exploré ici les formes (A x B) y (C z D) (c'est (8-5)*(7+1) ou (1+3)*(2-8) par exemple) et A x (B y C) z D (c'est 3*(2-1)*8 par exemple) ; mais pas A x B y (C z D) et (A x B) y C z D ! Il s'agit d'une part d'un jet rapide, et d'autre part ce ne serait pas pertinent en shell car je soupçonne qu'il y aura des doublons et/ou même des triplons. Cependant, avec ces ajouts, on devrait arriver aux trois mille septante douze…

Petit bémol cependant : les calcul ici sont fait sur des entiers et c'est problématique pour les divisions car le hollandais volant l'entend flottant… (si j'en crois la fonction randomizeNumbers() qui pourtant fait un Math.floor(), à moins que ce ne soit à cause du evalMath(cell1, operator, cell2) dans la fonction evalResultat() ?) Je pense pouvoir corriger cela facilement, ce qui réduira le nombre de solutions proposées.

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par le_poney (Mastodon) le 24 février 2022 à 10:31. Évalué à 2.

Il ne manque pas également →
Par exemple avec 7 7 1 2 je m'attends au résultat ((7*7)-1)/2 alors qu'avec ce script je vais avoir 7*7=49; 1*2=2; 49/2=24 ce qui est un peu simplifié ?
- [^] # Re: un petit peu plus (de divisions)
  
  Posté par Gil Cot ✔ (site web personnel, Mastodon) le 24 février 2022 à 14:08. Évalué à 2. Dernière modification le 24 février 2022 à 14:08.
  
  Il ne manque pas également →
  
  Avec les commutativités (additions et multiplications) et les priorités (multiplications et divisions) on devrait retomber sur l'un des 4 cas précédemments énumérés…
  Mais je dis ça au doigt mouillé ; faudrait que je prenne le temps faire la preuve mathématique.
  
  Par exemple avec 7 7 1 2 je m'attends au résultat ((7*7)-1)/2
  
  Justement avec les priorités, ((7*7)-1)/2 est (7*7-1)/2 ; ce qui me fait dire qu'il manque éventuellement les cas (solutions5) et (solutions6) ainsi que (solutions0) tout simplement ?
  On peut facilement les rajouter… Le plus dur étant en fait, de détecter pour chaque type de solutions les divisions par zéro…
  
  “It is seldom that liberty of any kind is lost all at once.” ― David Hume
  - [^] # Re: un petit peu plus (de divisions)
    
    Posté par Gil Cot ✔ (site web personnel, Mastodon) le 25 février 2022 à 01:41. Évalué à 2. Dernière modification le 25 février 2022 à 01:42.
    Les quatre manquants sont rajoutés, ce qui porte le nombre de formes explorées à 6.
    Je croise les doigts ; on ne devrait pas avoir d'erreur de division.
    Consultation/Téléchargement → https://framagit.org/-/snippets/6519
    
    Par contre, comme il n'y a pas de table de sauvegarde intermédiaire, je ne sais trop comment élimer les doublons pour l'instant. Faudra filtrer soi-même les résultats :
```
$ ./trouve24.sh 7 7 1 2 | sort | uniq
```
    Je m'attaque à l'autre grand problème (ne retenir que les divisions entières) demain.
    
    “It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par steph1978 le 24 février 2022 à 10:50. Évalué à 2. Dernière modification le 24 février 2022 à 10:53.

cool une version bash

J'ai essayé de recoller tous les bouts. J'ai encore des /0 et process2 n'est jamais utilisé ; et je ne comprends pas le "$7" dans solution2.

Mais le plus gênant est quand même l'arrondi des divisions, cela ne respecte pas les règles du jeux donc ce n'est pas très utilisable. C'est pour ces raisons que je ne l'ai pas implémenté, trop de cas tordus.

[^] # Re: un petit peu plus (de divisions)

Posté par steph1978 le 24 février 2022 à 11:19. Évalué à 2.

(ok, je viens de comprendre les $6, $7, my bad)

J'ai fait une version "épurée" car j'aime bien l'approche mix de parenthèses et permutations des nombres.

[^] # Re: un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 24 février 2022 à 16:01. Évalué à 2.

J'ai essayé de recoller tous les bouts.

Désolé, je n'ai pas encore eu le temps de mettre en ligne, j'ai priorisé le commentaire expliquant l'approche à mon code jetable (il faudrait nettoyer un peu plus pour que ce soit présentable… bon, j'ai rajouté des commentaires à l'instant …parce-que des fonctions dont on n'a pas la signature ça va être dur à maintenir)

C'est maintenant en ligne https://framagit.org/-/snippets/6519

J'ai fait une version "épurée" car j'aime bien l'approche mix de parenthèses et permutations des nombres.

Ouf, mes explications ici ont été assez claires pour permettre de reconstituer l'ensemble …et l'adapter/épurer (ne pas s'enquiquiner avec les divisions)

Mais le plus gênant est quand même l'arrondi des divisions, cela ne respecte pas les règles du jeux donc ce n'est pas très utilisable.

Les règles n'étaient pas très claires pour moi. :-S Pour une fois que je n'ai pas voulu chipoter (et ai supposé qu'on faisait tous les calculs dans $\mathbb{N}$ …à tort) Il a fallu être devant le cas (en testant en ligne) pour se rendre compte que la page donnait des résultats en flottants. Du coup je suis allé jeter un œil au source de la page (heureusement tout est en JS et pas caché, mais mon ECMAScript est un peu rouillé et je n'ai pas su voir/dire si c'est intentionnel ou si c'est une erreur de codage : seul-e l'auteur-e peut le dire)

Je vais corriger cela dans une v2 dans l'une des manières suivantes (à voir ce qui est plus simple en shell)

Soit au moment du calcul on sait dire que la division ne sera pas entière (tester s'il y a un reste ?) et donc on squeeze (ce qui fait un cas computed en moins dans l'exploration)
Soit au niveau de la solution on s'assure (par un calcul dans $\mathbb{D}$ dans mon idée immédiat, et qu'il faudrait essayer de restreindre seulement aux cas où il y a un opérateur de division) qu'on retombe sur nos pattes… (si la vérification n'est pas concluante on aura eu un computed mais toujours pas de solved bien qu'étant arrivé dans la fonction d'affichage)

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 26 février 2022 à 00:37. Évalué à 3.

Bon, comme je disais plus tôt, j'ai rajouté les cas manquants en faisant attention aux divisions par zéro :-D Le nombre de résultats, par rapport à la vingtaine d'hier est multiplié par 3.8 ;-P

id	formule type	`1 2 3 8`	`7 7 1 2`
b3	`AxByCzD`	6	14
b1	`Ax(ByC)zD`	4	8
b2	`(AxB)y(CzD)`	16	14
r1	`AxBy(CzD)`	10	10
r2	`Ax(ByCzD)`	12	2
l1	`(AxB)yCzD`	8	14
l2	`(AxByC)zD`	12	16
all	total	68	78

Ensuite, comme promis hier, j'ai viré les solutions qui ne sont pas valides suite au constat. J'ai opté pour le faire au niveau de l'affichage des résultats car ça passe par l'appel de deux processus externes (jusque là, mis à part test qui peut être interne ou pas, tout était fait directement par le shell) qui sont dc (que je préfère à sa surcouche bc) et grep. Comme on pouvait s'y attendre, il y a moins de monde à l'arrivée… :-D

id	formule type	`1 2 3 8`	`7 7 1 2`
b3	`AxByCzD`	0	0
b1	`Ax(ByC)zD`	4	0
b2	`(AxB)y(CzD)`	10	0
r1	`AxBy(CzD)`	4	0
r2	`Ax(ByCzD)`	6	0
l1	`(AxB)yCzD`	2	0
l2	`(AxByC)zD`	6	2
all	total	32	2
all	calcul	10370	10378

Comme tu verras plus loin, avec l'implémentation en Python, il y a le cas intéressant de 1 4 5 6 pour lequel le script shell ne trouve pas de solution non plus (en fait on fait maintenant l'impasse sur le genre de solution invalide qui était proposé avant —testé et ça le fait.) Du coup, le défi suivant est de lui faire trouver l'élégante solution qui montre qu'on ne peut pas faire l'impasse sur la division…)
À suivre.

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 26 février 2022 à 20:24. Évalué à 3.

Comme tu verras plus loin, avec l'implémentation en Python, il y a le cas intéressant de 1 4 5 6 pour lequel le script shell ne trouve pas de solution non plus ([…]) Du coup, le défi suivant est de lui faire trouver l'élégante solution ([…])

On remet l'œuvre sur l'établi, et on fait la vérification en amont de la procédure d'affichage. Normalement le calcul doit se dérouler sans accroc parce que les cas tordus (pour l'instant les zéros et je n'en vois pas d'autres) ont été éliminés juste avant. On va faire appel à un programme externe pour quasiment tous les calculs, histoire qu'ils se fassent dans $\mathbb{D}$ et non plus $\mathbb{N}$ .
Comme je le craignais, lancer des processus a un certain coût qui est quand même important sur la machine où j'ai travaillé. Ainsi, par exemple pour 8 3 2 1 avec juste l1, je note que real/user/sys passe

de 0m0.109s/0m0.073s/0m0.040s (ancienne version)
à 0m4.503s/0m2.242s/0m3.984s (nouvelle version)
soit 41/30/99 fois plus de temps…

Ceci dit, ça reste intéressant car il faut moins d'une minute pour lister toutes les solutions possibles sur les pistes explorées. Le fait de changer de domaine de calcul ramène plus de résultats… (cela me fait penser à la programmation linéaire, sauf que c'est dans l'autre sens ; c'est peut-être une forme d'optimisation de production qui sait ? Mais revenons à nos moutons…)

id	type formule	`1 2 3 8`	`1 2 7 7`	`1 4 5 6`
b1	`Ax(ByC)zD`	10/1296	0/1320	0/1296
b2	`(AxB)y(CzD)`	10/1488	0/1480	0/1488
b3	`AxByCzD`	8/1536	2/1536	0/1536
l1	`(AxB)yCzD`	8/1536	2/1536	0/1536
l2	`(AxByC)zD`	8/1536	2/1536	0/1536
r1	`AxBy(CzD)`	10/1536	0/1520	0/1536
r2	`Ax(ByCzD)`	8/1530	0/1520	1/1524
all	totaux	62/10458	6/10448	1/10452

Plus de résultats mais pas mal de duplications… Arriver à les anticiper et donc ne pas calculer inutilement (ce qui aurait quand même été le cas si on stockait les résultats pour au final n'en afficher que les occurrences uniques…) C'est une piste d'amélioration qui pourrait impacter positivement le temps d'exécution.
Si on prend le cas soumis par le_poney, il n'y a qu'une seule solution qui est trouvée dans deux branches branches mais en deux ou quatre fois pour chacune…

$ trouve24.sh 7 7 1 2
7*7=49; 49-1=48; 48/2=24; b3
7*7=49; 49-1=48; 48/2=24; l1
7*7=49; 49-1=48; 48/2=24; l1
7*7=49; 49-1=48; 48/2=24; b3
7*7=49; 49-1=48; 48/2=24; l1
7*7=49; 49-1=48; 48/2=24; l1
Found 6 solutions for 10448 computations.

La solution de le_poney est la seule possible… C'est une r2 qui se présente comme suit chez moi :

5/4=1.25; 1.25-1=.25; 6/.25=24; r2

Mission accomplie ; la solution en shell semble l'emporter sur les autres ;-) Plus qu'à l'optimiser.
(p.s. Je mettrai à jour le snippet plus tard)

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 02 mars 2022 à 01:02. Évalué à 3.

[3615 mavie]

soit 41/30/99 fois plus de temps…
[…]
Plus qu'à l'optimiser.

J'ai pu optimiser un peu en essayant de réduire les calculs qui étaient refaits plusieurs fois : maintenant on stocke ces valeurs (échange d'un peu de temps CPU par un chouia de RAM ahha) et ça porte son fruit.

arguments	real	user	sys
`1 2 3 8` old	0’31.546”	0’16.209”	0’26.335”
`1 1 3 8` new	2’34.099”	1’15.180”	2’07.548”
`1 2 7 7` old	0’31.369”	0’16.186”	0’26.573”
`1 2 7 7` new	2’34.225”	1’15.134”	2’07.486”
`1 5 7 8` old	0’31.556”	0’16.218”	0’26.919”
`1 5 7 8` new	2’34.688”	1’15.529”	2’07.782”
`1 4 5 6` old	0’31.442”	0’16.191”	0’26.819”
`1 4 5 6` new	2’33.411”	1’15.030”	2’06.635”

À noter que je n'ai pas fait plusieurs exécutions et tiré les moyennes ; je ne suis pas dans un contexte de benchmark mais un contexte d'optimisation de code. Justement, une étape suivante serait de faire du profilage (un vaste débat pour du shell…)
Bien. On note un effondrement des performances… /o\ Pourtant, j'ai réduit les appels à dc :

id	type formule	avant	après
b1	`Ax(ByC)zD`	2+1	3
b2	`(AxB)y(CzD)`	2+2	3
b3	`AxByCzD`	2+1	3
l1	`(AxB)yCzD`	2+1	3
l2	`(AxByC)zD`	2+1	3
r1	`AxBy(CzD)`	2+2	3
r2	`Ax(ByCzD)`	2+2	3
all	total	24	21

Certes pas de beaucoup… Surtout qu'en contrepartie j'ai augmenté les appels à tr (via une sous-évaluation du shell) :

id	type formule	avant	après
b1	`Ax(ByC)zD`	1	2*2
b2	`(AxB)y(CzD)`	0	2*2
b3	`AxByCzD`	1	2*2
l1	`(AxB)yCzD`	1	2*2
l2	`(AxByC)zD`	1	2*2
r1	`AxBy(CzD)`	0	2*2
r2	`Ax(ByCzD)`	1	2*2
all	total	5	28

Le mieux est vraiment l'ennemi du bien… /o\ Et comme on dit, faut pas chercher à optimiser trop tôt, et le script évolue encore.
Par ailleurs, j'ai revu les tests de garde-fous et ai viré ce qui n'avait de sens que lorsqu'on travaillait en $\textbb{N}$ . Donc on calcule plus de cas qu'avant… (un élément en plus de l'augmentation de consommation de ressource, et je n'ai refait les mesures qu'après avoir fait toutes ces modifications.)

id	type formule	`1 2 3 8`	`1 2 7 7`	`1 4 5 6`	`1 5 7 8`
b1	`Ax(ByC)zD`	10/1536	2/1520	0/1536	4/1536
b2	`(AxB)y(CzD)`	10/1488	0/1480	0/1488	4/1488
b3	`AxByCzD`	8/1536	2/1536	0/1536	4/1536
l1	`(AxB)yCzD`	8/1536	2/1536	0/1536	4/1536
l2	`(AxByC)zD`	8/1536	2/1536	0/1536	4/1536
r1	`AxBy(CzD)`	10/1536	0/1520	0/1536	4/1536
r2	`Ax(ByCzD)`	8/1530	0/1520	1/1524	4/1530
all	totaux	62/10698	8/10648	1/10692	28/10698

Et là on a une petite surprise…

Si on prend le cas soumis par le_poney, il n'y a qu'une seule solution qui est trouvée dans deux branches branches mais en deux ou quatre fois pour chacune…

Eh non, il y a une seconde solution…
console $ trouve24.sh 7 7 1 2 2/7=.28; 7/.28=25.00; 25.00-1=24; B1 7*7=49; 49-1=48; 48/2=24; B3 7*7=49; 49-1=48; 48/2=24; L1 7*7=49; 49-1=48; 48/2=24; L2 2/7=.28; 7/.28=25.00; 25.00-1=24; B1 7*7=49; 49-1=48; 48/2=24; B3 7*7=49; 49-1=48; 48/2=24; L1 7*7=49; 49-1=48; 48/2=24; L2 Found 8 solutions for 10648 computations.

…qui, un peu similaire à un autre cas, se traduit par 7/(2/7)-1 (forme B1) ou… $ $\frac{7}{\frac{2}{7}}-1$ $

Bon, faudra peut-être augmenter la précision de calcul ?

$ dc -e '2k2 7/p'
.28
$ dc -e '18k2 7/p'
.285714285714285714

En fait c'est $0.\underline{285714}$
et on peut sentir que c'est faux même si ça tombe juste malgré les erreurs qui s'annulent (est-ce lié à l'usage de la virgule fixe dans dc ?) En effet,

On ne peut rien contre ce genre de truc à partir du moment où le site lui-même travaille en flottants et non en entiers. C'est marrant/intrigant…

(p.s. Je mettrai à jour le snippet plus tard)

Je l'ai faite hier pour la monture dont je parle présentement (y a eu depuis d'autres améliorations dont je parlerai une autre fois).

Plus de résultats mais pas mal de duplications… Arriver à les anticiper et donc ne pas calculer inutilement (ce qui aurait quand même été le cas si on stockait les résultats pour au final n'en afficher que les occurrences uniques…) C'est une piste d'amélioration qui pourrait impacter positivement le temps d'exécution.

Je ferai un autre topo sur ce point plus tard.

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 02 mars 2022 à 20:57. Évalué à 2.

[3615 mavie]

[…]
suite

Plus de résultats mais pas mal de duplications… Arriver à les anticiper et donc ne pas calculer inutilement (ce qui aurait quand même été le cas si on stockait les résultats pour au final n'en afficher que les occurrences uniques…) C'est une piste d'amélioration qui pourrait impacter positivement le temps d'exécution.

Je ferai un autre topo sur ce point plus tard.

Il faut en fait distinguer deux cas de figure…

Le premier aspect, c'est que pour une même branche/forme, on a par exemple

7*7=49; 49-1=48; 48/2=24; B3
7*7=49; 49-1=48; 48/2=24; B3

…qui s'explique par les permutations des nombres A, B, C, D ! Dans l'exemple, on a A=7_1, B=7_2 puis A=7_2, B=7_1 :-D On le voit mieux sur cet autre exemple ( A=1, B=3 puis ) :

1 + 3 = 4; 4 + 8 = 12; 12 * 2 = 24; B3
3 + 1 = 4; 4 + 8 = 12; 12 * 2 = 24; B3

Comme on ne fait pas le stockage des résultats, il n'y a pas vraiment de correction possible …à moins de trouver une façon de s'assurer qu'on n'a pas de doublon dans les permutations. Sachant que les permutations sont maintenant générées et non plus manuellement listées, faut donc rajouter des tests bien sentis aux bons endroits.

 # initialement
explore_all $1 $2 $3 $4
explore_all $1 $2 $4 $3
explore_all $1 $3 $2 $4
explore_all $1 $3 $4 $2
explore_all $1 $4 $2 $3
explore_all $1 $4 $3 $2
explore_all $2 $1 $3 $4
explore_all $2 $1 $4 $3
explore_all $2 $3 $1 $4
explore_all $2 $3 $4 $1
explore_all $2 $4 $1 $3
explore_all $2 $4 $3 $1
explore_all $3 $1 $2 $4
explore_all $3 $1 $4 $2
explore_all $3 $2 $1 $4
explore_all $3 $2 $4 $1
explore_all $3 $4 $1 $2
explore_all $3 $4 $2 $1
explore_all $4 $1 $2 $3
explore_all $4 $1 $3 $2
explore_all $4 $2 $1 $3
explore_all $4 $2 $3 $1
explore_all $4 $3 $1 $2
explore_all $4 $3 $2 $1

 # maintenant
for i1 in 1 2 3 4
do
    for i2 in 1 2 3 4
    do
        test $i2 -eq $i1 && continue
        for i3 in 1 2 3 4
        do
            test $i3 -eq $i1 && continue
            test $i3 -eq $i2 && continue
            for i4 in 1 2 3 4
            do
                test $i4 -eq $i1 && continue
                test $i4 -eq $i2 && continue
                test $i4 -eq $i3 && continue
                # mettre les test de doublons ici ?
                explore_all "${!i1}" "${!i2}" "${!i3}" "${!i4}"
            done
        done
    done
done

Le second aspect est celui des diverses formes…
J'étais parti dans l'idée d'explorer les différents arbres et comme annoncé, « plusieurs arbres peuvent être équivalent à cause de la commutativité de l'addition et de la multiplication. » C'est le cas ici :

7*7=49; 49-1=48; 48/2=24; B3
7*7=49; 49-1=48; 48/2=24; L1
7*7=49; 49-1=48; 48/2=24; L2

Avec la priorité de la multiplication et de la division sur l'addition et la soustraction, mettre la première partie entre parenthèses (L1) revient au même que de ne pas mettre de parenthèses (B3) et faire séquentiellement les autres opérations… Si on met la parenthèse autour des deux premières opérations (L2) on aboutit aussi au même résultat… Ouch !
On ne peut malheureusement pas anticiper les formes égales dans notre approche exploratrice (puisqu'on était parti sur du brute force je le rappelle). Il aurait fallu lister (et catégoriser) toutes les combinaisons possibles (approche dite par tables) : c'est plus fastidieux mais plus efficace et rapide à terme. Je me note d'implémenter cela quand j'aurai un peu de temps (et si le fun y est toujours.) En l'état (approche exploratrice) on n'y peut rien :(

Ayant dit cela, le parcours par formes n'est pas compatible avec l'approche brutale qui aurait juste parcouru les opérations sans se préoccuper des formes : c'est ce que font les autres propositions (en Python et en Prolog pour l'instant), et cela correspond en fait à la forme B3 ! C'est donc la seule que devrait implémenter la variante épurée (code ci-après) et c'est la seule explorée par défaut par la nouvelle monture du script (le reste est laissé, accessible par des options, pour me permettra de satisfaire ma curiosité mathématique …et pour vérifier les cas moins triviaux où on n'a pas de solution B3.)

 # maintenant
for i1 in 1 2 3 4
do
    for i2 in 1 2 3 4
    do
        test $i2 -eq $i1 && continue
        for i3 in 1 2 3 4
        do
            test $i3 -eq $i1 && continue
            test $i3 -eq $i2 && continue
            for i4 in 1 2 3 4
            do
                test $i4 -eq $i1 && continue
                test $i4 -eq $i2 && continue
                test $i4 -eq $i3 && continue
                # ceci remplace le/la bloc/fonction process0
                for o1 in '+' '-' '*'
                do
                    for o2 in '+' '-' '*'
                    do
                        for o3 in '+' '-' '*'
                        do
                            r1=$(( ${!i1} $o1 ${!i2} ))
                            r2=$(( $r1    $o2 ${!i3} ))
                            test $(( $r2  $o3 ${!i4} )) -eq 24 &&
                            echo "${!i1}$o1${!i2}=$r1; $r1$o2 ${!i3}=$r2; $r2$o3${!i4}=24"
                        done
                    done
                done
            done
        done
    done
done

Le script devenant important d'une part (même si à fonctionnement équivalent j'ai réduit le nombre de lignes) et complexe (avec pilotage maintenant par des options) d'autre part, je l'ai déplacé dans un dépôt dédié. https://framagit.org/gilcot/trouve24 Cela me permet également de garder trace des différents essais (et donc de savoir ce qui a déjà été tenté lors des prochaines améliorations.)

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: un petit peu plus (de divisions)

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 24 février 2022 à 15:05. Évalué à 2.
cool une version bash

POSIX shell, j'insiste :-D Ça devrait fonctionner aussi dash/ash avec lequel je teste. C'est juste qu'on évite des trucs propres à bash/ksh??/pdksh/zsh/etc ; mais ce faisant on s'évite certaines facilités (comme les tableaux et certaines formes de tests)

J'ai encore des /0 […] ; et je ne comprends pas le "$7" dans solution2.

J'ai oublié de corriger mon post (rédigé certes offline pour avoir le temps de tester un peu et donc présenter un POC au lieu d'une théorie, mais j'ai du zapper dans les aller-retours rédaction-débogage)
Dans la boucle for du second type type, j'avais mis deux tests (juste avant le calcul) au lieu du seul mentionné :
```
test "$o1" = '/' && test "$o3" = '/' && test $n2 -lt $n3 && continue
test "$o2" = '/' && test "$o3" = '/' && test $n2 -lt $n3 && continue
test $(( n1 $o1 (n2 $o3 n3) $o2 n4 )) -eq 24 &&
    solution2 "$n1" "$o1" "$n2" "$n3" "$o2" "$n4" "$o3"
```
J'ai ensuite remplacé les deux tests par un seul qui fusionne les deux…
```
test "$o3" = '/' && test $n2 -lt $n3 && continue
test $(( n1 $o1 (n2 $o3 n3) $o2 n4 )) -eq 24 &&
    solution2 "$n1" "$o1" "$n2" "$n3" "$o2" "$n4" "$o3"
```
Le $7 est $o3 ; mais on peut réarranger l'ordre si ça simplifie la lecture et la compréhension.

et process2 n'est jamais utilisé

Pas possible ! Je les ai testé séparément sur ton exemple et ça m'a bien renvoyé les quatre résultats (pour 1344 calculs) suivants :
```
2-1=1; 3*1=3; 3*8=24
2-1=1; 3/1=3; 3*8=24
2-1=1; 8*1=8; 8*3=24
2-1=1; 8/1=8; 8*3=24
```
trop de cas tordus.

Oui et c'était le premier pan de mon défi :-D

Je viens d'en trouver un avec l'exemple de "le_poney" :-D (dans la sortie suivante, je n'ai activé que solutions2)
```
$ trouve24.sh 7 7 1 2
7*1=7; 7*7=49; 49/2=24
7/1=7; 7*7=49; 49/2=24
1*7=7; 7*7=49; 49/2=24
7*1=7; 7*7=49; 49/2=24
7/1=7; 7*7=49; 49/2=24
1*7=7; 7*7=49; 49/2=24
7*7=49; 1*49=49; 49/2=24
trouve24.sh: line 77: n1 / (n2 - n3) + n4 : division by 0 (error token is "+ n4 ")
```
C'est le cas 1 / (7 - 7) + 2 qui devrait pouvoir se corriger sans trop de difficulté. Je fais ça tout à l'heure.

“It is seldom that liberty of any kind is lost all at once.” ― David Hume
- [^] # Re: un petit peu plus (de divisions)
  
  Posté par Gil Cot ✔ (site web personnel, Mastodon) le 24 février 2022 à 16:09. Évalué à 2.
  
  C'est le cas 1 / (7 - 7) + 2
  
  Corrigé …par l'ajout d'un test supplémentaire que j'ai probablement zappé à cause de la fatigue.
  
  “It is seldom that liberty of any kind is lost all at once.” ― David Hume

# Python 3

Posté par 🚲 Tanguy Ortolo (site web personnel) le 25 février 2022 à 10:38. Évalué à 4.

En Python 3 :

#! /usr/bin/python3

import argparse


add = int.__add__
sub = int.__sub__
mul = int.__mul__
div = lambda a, b: a // b
signes = {add: '+', sub: '-', mul: '×', div: '/'}


class Operation:
    def __init__(self, a, b, op):
        self.a  = a
        self.b  = b
        self.op = op
        self._int = None

    def __int__(self):
        if self._int is None:
            self._int = self.op(int(self.a), int(self.b))
        return self._int

    def __str__(self):
        return '(%s %s %s)' % (self.a, signes[self.op], self.b)


# Génère toutes les opérations faisables avec deux entiers ou opérations
def operations(a, b):
    yield Operation(a, b, add)
    yield Operation(a, b, mul)
    yield Operation(a, b, sub)
    if int(b) != 0 and int(a) % int(b) == 0:
            yield Operation(a, b, div)


# Génère tous les calculs faisables avec des entiers ou opérations
def calculs(*termes):
    l = len(termes)
    if l == 1:
        # Un seul terme, rien à faire à part le renvoyer tel quel !
        yield termes[0]
    else:
        # Au moins deux termes: on en prend un…
        for i in range(l):
            a = termes[i]
            # … puis un autre
            for j in range(l):
                if i == j:
                    # Pas le même !
                    continue
                b = termes[j]
                # On parcours les opérations possibles entre eux
                for ab in operations(a, b):
                    # On considère le résultat de cette opération comme un nouveu terme
                    # remplaçant les deux choisis.
                    yield from calculs(ab, *[termes[k] for k in range(l) if k != i and k != j])


def trouve(nombres, target):
    for calcul in calculs(*nombres):
        if int(calcul) == target:
            yield calcul


def main(args=None):
    parser = argparse.ArgumentParser(description="Trouve un ou des moyens d'obtenir 24 avec les nombres donnés")
    parser.add_argument("--all", action='store_true', help="affiche tous les calculs donnant ce résultat, plutôt que seulement le premier trouvé")
    parser.add_argument("--target", type=int, default=24, help="cherche un résultat autre que 24")
    parser.add_argument("numbers", nargs='+', help="nombres à utiliser")
    args = parser.parse_args(args)
    calculs = trouve(args.numbers, args.target)
    for calcul in calculs:
        print('%s = %d' % (calcul, int(calcul)))
        if not args.all:
            break


if __name__ == '__main__':
    main()

Le site du jeu m'a proposé les nombres suivants : 1 4 5 6, ce qui m'amène à douter un peu de la garantie que « 100 % des parties ont une ou plusieurs solutions ».

[^] # Re: Python 3

Posté par le_poney (Mastodon) le 25 février 2022 à 17:45. Évalué à 2.

Par rapport à la solution de 1 4 5 6 -> 6/((5/4)-1)
Donc j'imagine qu'il y a des modifications à faire pour ton résolveur ;)

[^] # Re: Python 3

Posté par Cangamra le 25 février 2022 à 17:51. Évalué à 0.

il y a aussi la solution :
(6x4)+(1/5)
car en division entière 1/5 ça fait zéro
- [^] # Re: Python 3
  
  Posté par Gil Cot ✔ (site web personnel, Mastodon) le 25 février 2022 à 18:43. Évalué à 3.
  
  Attention, dans mon implémentation en shell, j'ai naïvement cru que la division entière le ferait. Mais comme je le mentionne dans un commentaire, le site ne l'entend pas de cette oreille.
  
  “It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: Python 3

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 25 février 2022 à 18:57. Évalué à 2.

6/((5/4)-1)

Euh… je traduis par :

Ce qui donne bien :

$ dc -e '5k5 4/1-6r/p'
24.00000

(contrairement à mon intuition en commençant ce message)
C'est bluffant… mais logique :

$ dc -e '5k5 4/1-6rf'
.25000
6

(diviser par le quart revient à multiplier par quatre)

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: Python 3

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 25 février 2022 à 19:59. Évalué à 2. Dernière modification le 25 février 2022 à 19:59.
Je crois que je viens de comprendre…
```
    if int(b) != 0 and int(a) % int(b) == 0:
            yield Operation(a, b, div)
```
Nous avons tous compris qu'on fait des divisions entières… Du coup, ici, il ne poursuit pas avec $\frac{5}{4}$ ! Et moi, dans l'implémentation Shell, j'ai fait directement les calculs entiers (i.e. $\mathbb{N}\to\mathbb{N}$ ) et donc sauté cette combinaison
```
$ echo $(( 6/((5/4)-1) ))
-bash: 6/((5/4)-1) : division by 0 (error token is " ")
$ echo $(( (5/4)-1 ))
0
```
“It is seldom that liberty of any kind is lost all at once.” ― David Hume
[^] # Re: Python 3

Posté par 🚲 Tanguy Ortolo (site web personnel) le 28 février 2022 à 10:12. Évalué à 4.

Bien vu. Il me faut utiliser des rationnels. Je vais voir ce que je peux faire pour ça.

[^] # Re: Python 3

Posté par 🚲 Tanguy Ortolo (site web personnel) le 28 février 2022 à 11:02. Évalué à 5.

Correction, en utilisant les rationnels du module standard fractions :

#! /usr/bin/python3

import argparse
from fractions import Fraction


add = Fraction.__add__
sub = Fraction.__sub__
mul = Fraction.__mul__
div = Fraction
signes = {add: '+', sub: '-', mul: '×', div: '/'}


class Operation:
    """An operation between two integers, fractions or operations"""
    def __init__(self, a, b, op):
        """Return an operation representing 'a op b':
           a, b  integers, fractions or operations
           op    operator"""
        self.a  = a
        self.b  = b
        self.op = op
        self._result = None

    def result(self):
        """Return the result of the operation, as a fraction"""
        if self._result is None:
            a = value(self.a)
            b = value(self.b)
            self._result = self.op(a, b)
        return self._result

    def __str__(self):
        return '(%s %s %s)' % (self.a, signes[self.op], self.b)


def value(a):
    """Return the value of an integer, a fraction, or the result of an operation"""
    if isinstance(a, Operation):
        return a.result()
    else:
        return a


def operations(a, b):
    """Yields of feasible operations between two integers, fractions or operations"""
    yield Operation(a, b, add)
    yield Operation(a, b, mul)
    yield Operation(a, b, sub)
    if value(b) != 0:
        yield Operation(a, b, div)


def calculs(*termes):
    """Yields all feasible computations with multiple integers or fractions"""
    l = len(termes)
    if l == 1:
        # Un seul terme, rien à faire à part le renvoyer tel quel !
        yield termes[0]
    else:
        # Au moins deux termes: on en prend un…
        for i in range(l):
            a = termes[i]
            # … puis un autre
            for j in range(l):
                if i == j:
                    # Ce sont les mêmes termes, ce n'est pas ce qu'on recherche
                    continue
                b = termes[j]
                # On parcours les opérations possibles entre eux
                for ab in operations(a, b):
                    # On considère le résultat de cette opération comme un nouveu terme
                    # remplaçant les deux choisis.
                    yield from calculs(ab, *[termes[k] for k in range(l) if k != i and k != j])


def trouve(nombres, target):
    """Yields all computations of multiple integers or fractions, which result in the given target"""
    for calcul in calculs(*nombres):
        if value(calcul) == target:
            yield calcul


def main(args=None):
    parser = argparse.ArgumentParser(description="Trouve un ou des moyens d'obtenir 24 avec les nombres donnés")
    parser.add_argument("--all", action='store_true', help="affiche tous les calculs donnant ce résultat, plutôt que seulement le premier trouvé")
    parser.add_argument("--target", type=int, default=24, help="cherche un résultat autre que 24")
    parser.add_argument("numbers", nargs='+', type=int, help="nombres à utiliser")
    args = parser.parse_args(args)
    calculs = trouve(args.numbers, args.target)
    for calcul in calculs:
        print('%s = %d' % (calcul, value(calcul)))
        if not args.all:
            break


if __name__ == '__main__':
    main()

[^] # Re: Python 3

Posté par 🚲 Tanguy Ortolo (site web personnel) le 28 février 2022 à 11:03. Évalué à 3.
Et pour les nombres cités :
```
% ./trouve.py 1 4 5 6
(6 / ((5 / 4) - 1)) = 24
```

[^] # Re: Python 3

Posté par steph1978 le 28 février 2022 à 15:06. Évalué à 2.

C'est pour moi la meilleure solution à date.
L'élégance du Python sûrement :)
Permet de résoudre trouve 24 et le compte est bon.

[^] # Re: Python 3

Posté par 🚲 Tanguy Ortolo (site web personnel) le 28 février 2022 à 15:23. Évalué à 4.

Ça pourrait être sympa en (O)Caml, aussi.

[^] # Re: Python 3

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 01 mars 2022 à 01:50. Évalué à 2. Dernière modification le 01 mars 2022 à 01:50.

En Haskell et en Lisp aussi (: Mais j'ai d'abord pensé à OCaml hier en lisant ton code.

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: Python 3

Posté par 🚲 Tanguy Ortolo (site web personnel) le 01 mars 2022 à 08:47. Évalué à 3.

C'est le besoin de type union qui m'a rappelé Caml, en rédigeant ça en Python, en fait.

[^] # Haskell

Posté par Anthony Jaguenaud le 04 mars 2022 à 18:20. Évalué à 3. Dernière modification le 04 mars 2022 à 19:37.

J’y ai pensé aussi, je l’ai fait. Je ne suis pas un pro du haskell, soyez bienveillant avec vos remarques ;-)

import Data.List

-- A value is an Int or an operation with two arguments and a result.
data Value = V Int | Op Operation Value Value Int
data Operation = Plus | Min | Mult | Div | Error

-- Instance of Show class to be able to display Operation type
instance Show Operation where
  show Plus = "+"
  show Min  = "-"
  show Mult = "×"
  show Div  = "÷"
  show _    = "Error"

-- Instance of Show class for Value.
instance Show Value where
  show (V a) = show a
  show (Op o a b _) = " (" ++ (show a) ++ (show o) ++ (show b) ++ ") "

-- Take an Operation and a list of 2 minimal Values. Generate a new value with the first two terms.
doOp :: Operation -> [Value] -> [Value]
doOp Plus (a:b:xs) = (Op Plus a b (va+vb):xs)
                      where va = getV a
                            vb = getV b
-- We don't want to have negative values, so check if a >= b
doOp Min (a:b:xs) | (getV a) >= (getV b) = (Op Min a b ((getV a)-(getV b)):xs)
                   | otherwise = (Op Error a b (-1)):xs
doOp Mult (a:b:xs) = (Op Mult a b (va*vb)):xs
                      where va = getV a
                            vb = getV b
-- First check that divisor is not 0, then check if b can divide a without rest.
doOp Div (a:b:xs) | vb == 0 = (Op Error a b (-1)):xs
                  | va `mod` vb == 0 = (Op Div a b (va `div` vb)):xs
                  | otherwise = (Op Error a b (-1)):xs
                   where va = getV a
                         vb = getV b

setV a = V a
getV (V a) = a
getV (Op _ _ _ a) = a


-- Do operations, take a list of Values and do all operations, drop error if a computation is not possible
doOps :: [Value] -> [[Value]]
doOps a = filter (dropError.head) $ map (\x -> doOp x a) [Plus, Min, Mult, Div] 

-- Check for error filter, return True if it's valid.
dropError :: Value -> Bool
dropError (Op Error _ _ _) = False
dropError _ = True

-- En entrée une liste de values, en sortie une liste d'opérations filtrée.
-- Check we have 4 numbers.
-- From right to left
--    - map setV x  => generate a Value list with only V values.
--    - compute all permutations
--    - For each list of values apply all operations on first two values, we get list of list of list so concat to obtain list of list Values
--    - We have 3 elements
--    - For each element, we perform permutations and concat to get a list of list of Values.
--    - loop twice to get list of list of Value with length == 1.
--    - Then filter to check if result is 24.
get24 :: [Int] -> [[Value]]
get24 x | length x == 4 = filter (\x -> (getV (head x))==24) $ concat.map doOps $ concat.map permutations $ concat.map doOps $ concat.map permutations $ concat.map doOps $ permutations $ map setV x
        | otherwise = []

Et les résultats :

*Main Data.List> :l try24.hs
[1 of 1] Compiling Main             ( try24.hs, interpreted )
Ok, one module loaded.
*Main Data.List> get24 [ 7,7,1,2]
[[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ]]
*Main Data.List> get24 [ 1,2,3,8]
[[ ( ( (2-1) ×3) ×8) ],[ (8× ( (2-1) ×3) ) ],[ ( (3× (2-1) ) ×8) ],[ (8× (3× (2-1) ) ) ],[ ( (3÷ (2-1) ) ×8) ],[ (8× (3÷ (2-1) ) ) ],[ ( (8×3) × (2-1) ) ],[ ( (8×3) ÷ (2-1) ) ],[ ( (2-1) × (8×3) ) ],[ ( (3×8) × (2-1) ) ],[ ( (3×8) ÷ (2-1) ) ],[ ( (2-1) × (3×8) ) ],[ ( (8× (2-1) ) ×3) ],[ (3× (8× (2-1) ) ) ],[ ( (8÷ (2-1) ) ×3) ],[ (3× (8÷ (2-1) ) ) ],[ ( ( (2-1) ×8) ×3) ],[ (3× ( (2-1) ×8) ) ],[ ( (8-2) × (3+1) ) ],[ ( (3+1) × (8-2) ) ],[ ( (8+ (3+1) ) ×2) ],[ (2× (8+ (3+1) ) ) ],[ ( ( (3+1) +8) ×2) ],[ (2× ( (3+1) +8) ) ],[ ( (8-2) × (1+3) ) ],[ ( (1+3) × (8-2) ) ],[ ( (8+ (1+3) ) ×2) ],[ (2× (8+ (1+3) ) ) ],[ ( ( (1+3) +8) ×2) ],[ (2× ( (1+3) +8) ) ],[ ( (1+ (8+3) ) ×2) ],[ (2× (1+ (8+3) ) ) ],[ ( ( (8+3) +1) ×2) ],[ (2× ( (8+3) +1) ) ],[ ( (2-1) × (8×3) ) ],[ ( (8×3) × (2-1) ) ],[ ( (8×3) ÷ (2-1) ) ],[ ( (1+ (3+8) ) ×2) ],[ (2× (1+ (3+8) ) ) ],[ ( ( (3+8) +1) ×2) ],[ (2× ( (3+8) +1) ) ],[ ( (2-1) × (3×8) ) ],[ ( (3×8) × (2-1) ) ],[ ( (3×8) ÷ (2-1) ) ],[ ( (1+3) × (8-2) ) ],[ ( (8-2) × (1+3) ) ],[ ( (3+1) × (8-2) ) ],[ ( (8-2) × (3+1) ) ],[ ( (3+ (8+1) ) ×2) ],[ (2× (3+ (8+1) ) ) ],[ ( ( (8+1) +3) ×2) ],[ (2× ( (8+1) +3) ) ],[ ( (3+ (1+8) ) ×2) ],[ (2× (3+ (1+8) ) ) ],[ ( ( (1+8) +3) ×2) ],[ (2× ( (1+8) +3) ) ],[ ( (3+1) × (8-2) ) ],[ ( (8-2) × (3+1) ) ],[ ( (1+3) × (8-2) ) ],[ ( (8-2) × (1+3) ) ],[ ( ( (2-1) ×8) ×3) ],[ (3× ( (2-1) ×8) ) ],[ ( (8× (2-1) ) ×3) ],[ (3× (8× (2-1) ) ) ],[ ( (8÷ (2-1) ) ×3) ],[ (3× (8÷ (2-1) ) ) ],[ ( (3×8) × (2-1) ) ],[ ( (3×8) ÷ (2-1) ) ],[ ( (2-1) × (3×8) ) ],[ ( (8×3) × (2-1) ) ],[ ( (8×3) ÷ (2-1) ) ],[ ( (2-1) × (8×3) ) ],[ ( (3× (2-1) ) ×8) ],[ (8× (3× (2-1) ) ) ],[ ( (3÷ (2-1) ) ×8) ],[ (8× (3÷ (2-1) ) ) ],[ ( ( (2-1) ×3) ×8) ],[ (8× ( (2-1) ×3) ) ],[ ( ( (8+1) +3) ×2) ],[ (2× ( (8+1) +3) ) ],[ ( (3+ (8+1) ) ×2) ],[ (2× (3+ (8+1) ) ) ],[ ( ( (1+8) +3) ×2) ],[ (2× ( (1+8) +3) ) ],[ ( (3+ (1+8) ) ×2) ],[ (2× (3+ (1+8) ) ) ],[ ( ( (1+3) +8) ×2) ],[ (2× ( (1+3) +8) ) ],[ ( (8+ (1+3) ) ×2) ],[ (2× (8+ (1+3) ) ) ],[ ( (8-2) × (1+3) ) ],[ ( (1+3) × (8-2) ) ],[ ( ( (8+3) +1) ×2) ],[ (2× ( (8+3) +1) ) ],[ ( (1+ (8+3) ) ×2) ],[ (2× (1+ (8+3) ) ) ],[ ( (2-1) × (8×3) ) ],[ ( (8×3) × (2-1) ) ],[ ( (8×3) ÷ (2-1) ) ],[ ( ( (3+8) +1) ×2) ],[ (2× ( (3+8) +1) ) ],[ ( (1+ (3+8) ) ×2) ],[ (2× (1+ (3+8) ) ) ],[ ( (2-1) × (3×8) ) ],[ ( (3×8) × (2-1) ) ],[ ( (3×8) ÷ (2-1) ) ],[ ( ( (3+1) +8) ×2) ],[ (2× ( (3+1) +8) ) ],[ ( (8+ (3+1) ) ×2) ],[ (2× (8+ (3+1) ) ) ],[ ( (8-2) × (3+1) ) ],[ ( (3+1) × (8-2) ) ]]

Évidemment, on prend toute les permutations d’une même solution.

[^] # Re: Haskel

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 04 mars 2022 à 19:03. Évalué à 2.

PS Un admin pour changer le titre de « Re: Python 3 » en « Haskel » ? (bien que ce soit toujours le même fil, c'est plus sympa pour voir les déviations et parenthèses)

Merci beaucoup pour la contribution à la Fédération Trouve Vingt-Quatre :D
Oui, les doublons du fait de toutes les permutations sont un problème connu et normal/prévisible…
Sinon, as-tu testé le fameux cas get24 [ 1,4,5,6] ? ;-)

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: Haskell

Posté par Benoît Sibaud (site web personnel) le 04 mars 2022 à 19:39. Évalué à 4.

Fait.

[^] # Re: Haskel

Posté par Anthony Jaguenaud le 04 mars 2022 à 20:26. Évalué à 2. Dernière modification le 04 mars 2022 à 20:27.

Non, je n'avait pas testé…

*Main> get24 [ 1,4,5,6] 
[]
*Main>

Il retourne une liste vide, donc sans solution du point de vue de mon programme… c'est le résultat attendu ?

[^] # Re: Haskel

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 04 mars 2022 à 20:46. Évalué à 2. Dernière modification le 04 mars 2022 à 20:48.

Héhé c'est pour ça que c'est un fameux cas… La solution est 6/((5/4)-1)
https://linuxfr.org/users/steph1978/journaux/resoudre-trouve-24#comment-1884537

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

[^] # Re: Haskel

Posté par Anthony Jaguenaud le 04 mars 2022 à 23:38. Évalué à 2. Dernière modification le 04 mars 2022 à 23:38.

Oui, mais j'ai volontairement omis les nombres à virgules…

I’ll be back with Rational soon ;-)

[^] # Re: Haskel

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 05 mars 2022 à 00:52. Évalué à 2.

Oui, remplacer div par % et adapter les tests dans doOp Div (a:b:xs) :-)

Mais fais gaffe aussi à ne pas jeter trop vite les négatifs dans doOp Min (a:b:xs) …parce-que le produit ou la divisions de deux négatifs donnent un positif d'une part, et que l'ajout d'un négatif à un truc plus grand que 24 t'en rapproche. Je vois si je te retrouve un des cas sur lesquels j'étais tombé comme ça.

“It is seldom that liberty of any kind is lost all at once.” ― David Hume
- [^] # Re: Haskel
  
  Posté par Anthony Jaguenaud le 05 mars 2022 à 09:36. Évalué à 2.
  Oui, remplacer div par % et adapter les tests dans doOp Div (a:b:xs) :-)
  
  Non, ça ne marchera pas.
```
:t (/)
(/) :: Fractional a => a -> a -> a
:t div
div :: Integral a => a -> a -> a
Prelude Data.Ratio> 1% 4
1 % 4
Prelude Data.Ratio> (1%4) `div` (4%5)

<interactive>:28:1: error:
    • Non type-variable argument in the constraint: Integral (Ratio a)
      (Use FlexibleContexts to permit this)
    • When checking the inferred type
        it :: forall a. (Integral a, Integral (Ratio a)) => Ratio a
```
  La division entière à besoin d’un type integral ce que n'est pas Ratio. On ne peut pas mélanger les types dans les divisions.

[^] # Re: Haskel

Posté par Anthony Jaguenaud le 05 mars 2022 à 10:03. Évalué à 4.

Voilà la solution, j’ai changé les Int en Ratio Int, enlevé les vérifications de la division et de la soustraction (mais là, je n’en vois pas l’intérêt ;-) )

À chaque modification, j’ai laissé l’ancienne ligne en commentaire pour voir les différences.

import Data.List
-- new line
import Data.Ratio

-- A value is an Int or an operation with two arguments and a result.
--data Value = V Int | Op Operation Value Value Int
data Value = V (Ratio Int) | Op Operation Value Value (Ratio Int)
data Operation = Plus | Min | Mult | Div | Error

-- Instance of Show class to be able to display Operation type
instance Show Operation where
  show Plus = "+"
  show Min  = "-"
  show Mult = "×"
  show Div  = "÷"
  show _    = "Error"

-- Instance of Show class for Value.
instance Show Value where
--  show (V a) = show a
  show (V a) = show $ numerator a  -- The value is a % 1
  show (Op o a b _) = " (" ++ (show a) ++ (show o) ++ (show b) ++ ") "

-- Take an Operation and a list of 2 minimal Values. Generate a new value with the first two terms.
doOp :: Operation -> [Value] -> [Value]
doOp Plus (a:b:xs) = (Op Plus a b (va+vb):xs)
                      where va = getV a
                            vb = getV b
-- We don't want to have negative values, so check if a >= b
-- We work in ℚ
doOp Min (a:b:xs) = (Op Min a b ((getV a)-(getV b)):xs)
--                   | otherwise = (Op Error a b (-1)):xs
doOp Mult (a:b:xs) = (Op Mult a b (va*vb)):xs
                      where va = getV a
                            vb = getV b
-- First check that divisor is not 0, then check if b can divide a without rest.
doOp Div (a:b:xs) | vb == 0 = (Op Error a b (-1)):xs
--                  | va `mod` vb == 0 = (Op Div a b (va `div` vb)):xs
--                  | otherwise = (Op Error a b (-1)):xs
                  | otherwise = (Op Div a b (va / vb)):xs
                   where va = getV a
                         vb = getV b

-- Create a Ratio
--setV a = V a
setV a = V (a % 1)
getV (V a) = a
getV (Op _ _ _ a) = a


-- Do operations, take a list of Values and do all operations, drop error if a computation is not possible
doOps :: [Value] -> [[Value]]
doOps a = filter (dropError.head) $ map (\x -> doOp x a) [Plus, Min, Mult, Div] 

-- Check for error filter, return True if it's valid.
dropError :: Value -> Bool
dropError (Op Error _ _ _) = False
dropError _ = True

-- En entrée une liste de values, en sortie une liste d'opérations filtrée.
-- Check we have 4 numbers.
-- From right to left
--    - map setV x  => generate a Value list with only V values.
--    - compute all permutations
--    - For each list of values apply all operations on first two values, we get list of list of list so concat to obtain list of list Values
--    - We have 3 elements
--    - For each element, we perform permutations and concat to get a list of list of Values.
--    - loop twice to get list of list of Value with length == 1.
--    - Then filter to check if result is 24.
get24 :: [Int] -> [[Value]]
get24 x | length x == 4 = filter (\x -> (getV (head x))==24) $ concat.map doOps $ concat.map permutations $ concat.map doOps $ concat.map permutations $ concat.map doOps $ permutations $ map setV x
        | otherwise = []

Et le résultat :

*Main Data.Ratio> get24 [7,7,2,1]
[[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ]]
*Main Data.Ratio> get24 [ 1,4,5,6]
[[ (6÷ ( (5÷4) -1) ) ],[ (4÷ (1- (5÷6) ) ) ],[ (6÷ ( (5÷4) -1) ) ],[ (4÷ (1- (5÷6) ) ) ]]
*Main Data.Ratio> get24 [7,7,2,1]
[[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ],[ ( ( (7×7) -1) ÷2) ]]
*Main Data.Ratio> get24 [ 1,4,5,6]
[[ (6÷ ( (5÷4) -1) ) ],[ (4÷ (1- (5÷6) ) ) ],[ (6÷ ( (5÷4) -1) ) ],[ (4÷ (1- (5÷6) ) ) ]]

[^] # Re: Haskel

Posté par Gil Cot ✔ (site web personnel, Mastodon) le 05 mars 2022 à 17:57. Évalué à 2.
Top ! C'est plus complet et le code a passé tous les tests :-D

Bien vu pour la seconde solution :

puis

C'est formellement correct mais ne serait pas passé sur le site, vu que le JS travaille en flottants (i.e. notation scientifique) et que $\frac{5}{6}=0.8\underline{3}$ → $1-\frac{5}{6}=1.\underline{6}$ (ptdr)
Ceci ne remet aucunement en cause ton programme qui trouve justement des solutions exactes qui passent sous le radar ailleurs (je me demande si on doit ouvrir un issue au hollandais volant ;D j'ai le même souci avec mon implémentation shell, qui elle travaille en décimale fixe…)

et de la soustraction (mais là, je n’en vois pas l’intérêt ;-) )

Si, si. Il faut que tu testes avec et sans le check sur les soustraction pour les valeurs 7,6,5,1
```
$ trouve24.sh -e b2 -k4 1 5 6 7
1 - 7 = -6; 5 * 6 = 30; -6 + 30 = 24;   
1 - 7 = -6; 6 * 5 = 30; -6 + 30 = 24;   
5 * 6 = 30; 1 - 7 = -6; 30 + -6 = 24;   
5 * 6 = 30; 7 - 1 = 6;  30 - 6 = 24;    
6 * 5 = 30; 1 - 7 = -6; 30 + -6 = 24;   
6 * 5 = 30; 7 - 1 = 6;  30 - 6 = 24;    
Found 6 solutions over 1488 computations.
```
Normalement, si j'ai bien compris, la contrainte imposée sur les soustractions rejetait qui pourtant permet d'arriver au résultat avec au final.
Autre exemple avec un effet similaire :
```
$ trouve24.sh -e l2 -k4 1 5 7 8
1 - 5 = -4; -4 + 7 = 3; 3 * 8 = 24; 
1 + 7 = 8;  8 - 5 = 3;  3 * 8 = 24; 
7 + 1 = 8;  8 - 5 = 3;  3 * 8 = 24; 
7 - 5 = 2;  2 + 1 = 3;  3 * 8 = 24; 
Found 4 solutions over 1536 computations.
```
“It is seldom that liberty of any kind is lost all at once.” ― David Hume
- [^] # Re: Haskel
  
  Posté par Anthony Jaguenaud le 05 mars 2022 à 19:25. Évalué à 2.
  
  En fait ta première ligne :((1-5) + 7 ) × 8 <=> ((7 - 5) + 1)×8. Solution que mon programme trouve. Il trouve également : (7-(5-1))×8.
  - [^] # Re: Haskel
    
    Posté par Gil Cot ✔ (site web personnel, Mastodon) le 05 mars 2022 à 20:44. Évalué à 2.
    Oui, je n'en disconvient pas et c'était pour donner des exemples où on a une différence négative (i.e. soustraction qui donne un résultat non positif). Et bien sûr il y a des solutions qui sont équivalentes puisqu'on ne fait que permuter les termes et que pour certains opérateurs ça ne change pas le résultat. Dans mon cas, voici ce qui est calculé (forme dite L2) :
    - première ligne l2 : (1-5+7)×8 avec calcul de 1-5 en premier
    - quatrième ligne l2 : (7-5+1)×8 avec calcul de 7-5 en premier
    Je n'ai pas présenté tous les résultats possibles sinon on a aussi (seulement qui font intervenir des différences négatives) :
    - l1 : (1-5+7)×8 avec calcul de 1-5 en premier
    - r2 : 8×(7+1-5) avec calcul de 7+1 en premier
    - r2 : 8×(1-5+7) avec calcul de 1-5 en premier, ce qui est exactement pareil que le précédent sauf que là pas de différence négative
    - b1 : (1-(5-7))×8
    - b1 : (7+(1-5))×8 qui revient exactement au même que le premier (L1)
    - b3 : (7+(1-5))×8 qui est la même que la précédente (B1, L1)
    L'autre résultat que tu mentionnes est donnée chez moi par le parcours B1 (c'est la quatrième ligne) et n'a pas de différence négative.
```
$ trouve24.sh -e b1 1 5 7 8
5 - 7 = -2; 1 - -2 = 3; 3 * 8 = 24; 
7 - 5 = 2;  1 + 2 = 3;  3 * 8 = 24; 
1 - 5 = -4; 7 + -4 = 3; 3 * 8 = 24; 
5 - 1 = 4;  7 - 4 = 3;  3 * 8 = 24; 
Found 4 solutions over 1536 computations.
```
    “It is seldom that liberty of any kind is lost all at once.” ― David Hume

Suivre le flux des commentaires

Note : les commentaires appartiennent à celles et ceux qui les ont postés. Nous n’en sommes pas responsables.