Au début de l’année 2020, alors que l’on commençait à entendre parler de quelques cas de pneumonie atypique dans la ville chinoise de Wuhan, deux chercheurs français, Gaëtan Leurent (Inria) et Thomas Peyrin (Nanyang Technological University, Singapour), publiaient la première collision à préfixes choisis sur l’algorithme de condensation cryptographique SHA-1, et démontraient la faisabilité d’une attaque contre la toile de confiance OpenPGP.
L’attaque, dénommée SHA-mbles (« chaos », « désordre »), est de toute beauté et son étude fournit une excellente occasion, en cette période de confinement, de se pencher sur diverses notions comme le format des certifications OpenPGP ou le fonctionnement des algorithmes de condensation.
Sommaire
- Description sommaire de l’attaque
- Anatomie d’un certificat OpenPGP
- De SHA-1 et des collisions
- L’attaque sur les certifications OpenPGP
- Quel impact ?
Description sommaire de l’attaque
Avant d’entrer dans les détails sur le fonctionnement de l’attaque, voyons au préalable ce qu’elle permet de faire exactement.
Mallory, l’attaquant, cherche à usurper l’identité d’Alice, en fabriquant une clef OpenPGP à son nom qu’il pourra utiliser par exemple pour signer des documents et convaincre une tierce personne que ces documents proviennent d’Alice.
Pour réaliser cette attaque, Mallory génère deux clefs : une clef A portant le nom d’Alice, et une clef B portant un autre nom. Il fait certifier la clef B par Charlie, puis copie la certification de Charlie sur la clef A au nom d’Alice. Le but de l’attaque est que quiconque faisant confiance à Charlie accepte la clef A comme étant réellement la clef d’Alice, alors qu’Alice est totalement étrangère à cette clef.
Normalement, la manipulation de Mallory, qui consiste à copier une certification d’une clef vers une autre, ne devrait pas être possible. Ou plutôt, elle est complètement possible (une certification n’est jamais qu’une suite d’octets après tout) mais le résultat ne devrait pas pouvoir être considéré comme légitime, de par le principe même de ce qu’est une certification. Quiconque vérifie les certifications portées par la fausse clef A devrait se rendre compte que la certification émise par Charlie n’est pas valable (puisque c’est la clef B que Charlie a certifiée). L’exploit de Leurent et Peyrin est de générer les clefs A et B de telle sorte qu’une certification sur la seconde est aussi une certification valable sur la première.
L’attaque vise l’algorithme de condensation SHA-1 et le format des clefs publiques OpenPGP. À ce titre, elle ne dépend pas d’une implémentation particulière du standard OpenPGP (GnuPG par exemple), c’est le standard lui‑même qui est vulnérable.
Anatomie d’un certificat OpenPGP
Les briques de base du format OpenPGP, tel que défini dans le RFC 4880, sont les paquets. Chaque paquet a une structure de type TLV (Tag, Length, Value), composée d’un octet indiquant le type de paquet (le tag), un ou plusieurs octets indiquant la taille (en octets) du contenu du paquet, et le contenu (ou valeur) du paquet proprement dit. Une suite de plusieurs paquets constitue un message OpenPGP.
Un exemple de message OpenPGP est une clef publique transférable (Transferable Public Key ou TPK), parfois aussi appelée « certificat OpenPGP », qui contient toutes les informations publiques nécessaires pour communiquer avec le détenteur d’une paire de clefs (c’est par exemple ce que produit la commande --export de GnuPG). Une clef publique transférable est composée des paquets suivants :
- un paquet de clef publique (Public‐Key Packet) contenant la partie publique de la clef maîtresse ;
- pour chaque identité associée à la clef :
- soit un paquet d’identifiant utilisateur (User ID Packet, contenant une chaîne au format
Nom (commentaire) <adresse de courriel>), soit un paquet d’attribut utilisateur (User Attribute Packet, contenant une photo au format JPEG), - un paquet de signature (Signature Packet) contenant une auto‐certification émise par la clef maîtresse,
- éventuellement, des paquets de signature contenant des certifications émises par des clefs tierces ;
- soit un paquet d’identifiant utilisateur (User ID Packet, contenant une chaîne au format
- pour chaque sous‑clef associée à la clef maîtresse :
- un paquet de sous‑clef publique (Public‐Subkey Packet) contenant la partie publique de la sous‑clef,
- un paquet contenant une signature d’attachement (Binding Signature), émise par la clef maîtresse.
Les certifications mentionnées servent à attester (« certifier ») qu’une identité donnée est associée à la clef maîtresse située dans le premier paquet, c’est‐à‐dire que la clef appartient à l’utilisateur identifié. Une certification est une signature calculée comme suit :
- on concatène le paquet de clef publique, le paquet contenant l’identité (User ID Packet ou User Attribute Packet), plus quelques métadonnées (p. ex. la date de signature) ;
- on condense le tout à travers une fonction de condensation choisie parmi celles prises en charge par le standard (typiquement de nos jours, SHA2-256 — mais SHA-1 peut aussi être utilisée) ;
- on exécute l’algorithme de signature sur le condensat ainsi généré, avec sa clef maîtresse privée (dans le cas d’une auto‐certification, il s’agit de la clef privée correspondant à la clef publique située dans le premier paquet du certificat) ;
- on empaquette le résultat de la signature dans un Signature Packet.
Si une clef est associée à plusieurs identités (par exemples plusieurs adresses de courriel, ou une adresse de courriel et une photo), chaque identité est certifiée indépendamment, en répétant la procédure ci-dessus pour chaque User ID Packet et chaque User Attribute Packet.
De SHA-1 et des collisions
Brièvement, une fonction de condensation (hash function) cryptographique comme SHA-1 a pour objectif de produire une valeur unique de taille fixe (le condensat, ou l’image) à partir d’une entrée arbitraire (la pré‑image), et doit avoir les propriétés suivantes : il doit être pratiquement infaisable de trouver deux pré‑images produisant le même condensat (résistance aux collisions), et il doit être pratiquement infaisable de trouver une pré‑image correspondant à un condensat donné (preimage resistance, qui n’a pas vraiment de traduction élégante à mon goût en français)1.
Dans le standard OpenPGP, la fonction SHA-1 a deux rôles distincts. Le premier est le calcul des empreintes des clefs au format v4 (le seul format courant aujourd’hui, le format v3 étant obsolète depuis des années), qui permettent d’identifier une clef de manière unique. L’utilisation de SHA-1 est ici obligatoire, le standard n’autorise pas l’emploi d’une autre fonction pour cet usage2, du moins pas sans changer le format des clefs (la prochaine version du standard OpenPGP introduira un format v5 où les empreintes seront calculées avec SHA2-256). Le deuxième rôle de SHA-1 est de participer aux opérations de signature, pour calculer le condensat des données à signer qui est ensuite passé à l’algorithme de signature. Pour cet usage, SHA-1 n’est qu’une des fonctions possibles, le standard autorise aussi toute la famille SHA2 (SHA-224, SHA-256, SHA-384 et SHA-512). Toutes les implémentations modernes utilisent SHA2-256 par défaut, mais il est toujours possible de choisir d’utiliser SHA-1.
Dans les (très) grandes lignes, SHA-1 fonctionne en découpant les données à condenser en blocs de 64 octets et en traitant chaque bloc les uns après les autres ; chaque nouveau bloc traité met à jour un état interne sur 160 bits, et le condensat final renvoyé par la fonction est cet état interne tel qu’il est une fois le dernier bloc traité.
Une collision est la production de deux documents (« documents » au sens large : dans ce contexte, toute suite d’octets est un document) au contenu différent mais pour lequel la fonction SHA-1 donne un condensat identique. Trouver une collision devrait normalement demander 280 opérations, ce qui en pratique est infaisable à l’heure actuelle. Néanmoins, des faiblesses de la fonction permettent de réduire ce nombre d’un facteur d’environ 100 000 (à ~263), ce qui rend la recherche de collisions réalisable en pratique — comme démontré par l’attaque SHAttered de Marc Stevens et ses collègues (2017).
Une conséquence du fonctionnement par bloc de la fonction SHA-1, importante pour l’attaque qui nous intéresse ici, est qu’une fois que vous avez trouvé deux documents produisant une collision, vous pouvez étendre ces documents avec des données arbitraires tout en préservant la collision, dès lors que vous ajoutez les mêmes données arbitraires à la fin de chaque document. Par exemple, si les chaînes « ALICE » et « BOBBY » sont une collision et ont le même condensat « X », alors les chaînes « ALICEAIMELESFRAISES » et « BOBBYAIMELESFRAISES » sont aussi une collision et auront un même condensat « Y ».
Un type particulier de collision est la collision à préfixes choisis (chosen‐prefix collision). Cela consiste à partir de deux documents (les préfixes) distincts — qui donnent donc chacun un condensat différent — et à ajouter des blocs à chacun d’eux de telle sorte que les condensats des documents résultant soient identiques, permettant ainsi « d’annuler » la différence de départ. C’est une collision de ce type que décrivent Leurent et Peyrin dans leur attaque. Je ne m’attarderai pas sur les détails mathématiques qui sous‐tendent la recherche de la collision — j’en serais bien incapable —, mais soulignerai seulement qu’ils démontrent qu’il est possible de trouver une collision après avoir ajouté dix blocs (640 octets ou 5 120 bits) à chaque préfixe, au prix de ~263.4 opérations nécessitant deux mois de calcul sur neuf cents processeurs graphiques NVIDIA (pour un coût de 75 000 US$).
L’attaque sur les certifications OpenPGP
Pouvoir générer une collision à préfixes choisis, c’est bien, mais encore faut‑il exploiter cette possibilité pour monter une attaque crédible et pratique contre OpenPGP. Là, Leurent et Peyrin quittent le domaine de la cryptographie pour entrer dans celui du hack, et c’est un hack de toute beauté qu’ils proposent.
Rappelons leur objectif : il s’agit de générer deux clefs OpenPGP A et B de telle sorte qu’une signature de certification sur la clef B soit aussi valable sur la clef A.
La clef A sera une clef RSA de 8 192 bits, et sera associée à l’identifiant utilisateur Alice <alice@example.com>. La clef B sera une clef RSA de 6 144 bits (on reviendra dans un instant sur le choix de ces tailles), et sera associée à deux identités : un identifiant utilisateur Bob <bob@example.com> et un attribut utilisateur (une image JPEG). Quand Charlie signera la clef B que lui présentera Mallory, et conformément à la procédure de certification décrite plus haut, il générera deux certifications distinctes : une calculée sur la concaténation de la clef B et de l’identifiant Bob <bob@example.com> (cette certification ne jouera aucun rôle dans le reste de l’attaque ; en fait, cet identifiant est seulement là pour rendre la clef conforme — le standard OpenPGP impose qu’une clef publique soit associée à au moins un identifiant utilisateur), et une calculée sur la concaténation de la clef B et de l’image JPEG — c’est cette certification que Mallory va réutiliser.
Le principe de l’attaque est de faire en sorte que la concaténation de la clef A et de l’identifiant Alice <alice@example.com> produise un condensat SHA-1 identique à celui produit par la concaténation de la clef B et de la photo. Comment ? D’une part, en cachant une copie de l’identifiant Alice <alice@example.com> dans la photo de Bob (en exploitant le fait que les analyseurs JPEG ignorent généralement tous les octets situés après le marqueur de fin d’image, 0xFFD9), et, d’autre part, en cachant le début de cette même photo à la fin de la clef A. Voilà pourquoi les deux clefs sont de tailles différentes (8 192 bits pour la clef A contre 6 144 bits pour la clef B) : il faut que la clef B et le début de la photo de Bob (jusqu’à l’identifiant caché à la fin de celle‑ci) fassent au total la même taille que la clef A.
Cette différence de taille pose un problème, toutefois : la taille de chaque clef figure au début de son paquet (on a vu plus haut qu’un paquet OpenPGP avait une structure de type étiquette, taille, valeur) ; puisque les deux clefs A et B ont des tailles différentes, leurs paquets respectifs commencent différemment et produisent donc un condensat SHA-1 différent. Il faut donc pouvoir réussir à « annuler » cette différence, c’est‑à‑dire générer une collision à partir de deux préfixes choisis — exactement ce que Leurent et Peyrin sont capables de faire !
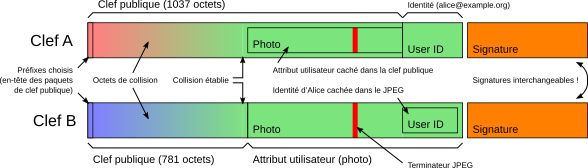
La figure ci‑dessus illustre le fonctionnement de l’attaque en résumant la composition des deux clefs A et B. Chaque clef commence par un préfixe différent (à cause de la différence de taille) ; puis viennent les blocs permettant d’établir la collision, c’est‑à‑dire de neutraliser la différence des préfixes. La collision est établie juste avant la fin du paquet contenant la clef publique B. Au‑delà de la collision, le contenu des deux clefs est identique, ce qui permet de préserver la collision et de garantir que les deux clefs produiront toujours un même condensat. La présence de la photo de Bob « cachée » dans le paquet de clef publique de la clef A est ignorée, car les octets correspondants sont simplement considérés comme faisant partie du module RSA ; dans la clef B, la présence de l’identifiant d’Alice « caché » dans la photo de Bob est ignorée, car il est situé après le marqueur de fin d’image JPEG.
Quel impact ?
Est‑ce qu’on va tous mourir ? Non. Enfin, si, mais pas à cause d’une collision à préfixes choisis sur SHA-1.
Si l’attaque est sérieuse et prouve encore, si besoin en était, que SHA-1 ne devrait plus être utilisé, l’impact sur OpenPGP devrait rester assez limité, en raison de plusieurs contraintes :
- Charlie, le signataire à qui Mallory demande de certifier la clef B, doit certifier avec l’algorithme de condensation SHA-1 obligatoirement ; s’il certifie avec un quelconque autre algorithme (comme SHA2-256, qui est l’algorithme utilisé par défaut par les versions modernes de GnuPG), l’attaque est inopérante, et ce paramètre est a priori hors du contrôle de Mallory ;
- les victimes de Mallory (celles à qui il présentera la fausse clef d’Alice) doivent accepter les certifications utilisant SHA-1, la version 2.2.18 de GnuPG refuse de telles certifications — précisément, suite à la révélation de cette attaque (référence CVE-2019-14855) —, toutefois les versions plus anciennes les acceptent sans sourciller (message pas subliminal : mettez à jour) ;
- le plus important à mon sens : l’attaque suppose que les victimes se reposent exclusivement sur la toile de confiance, c.‑à‑d. sur la certification de Charlie, pour valider la clef que Mallory leur présente comme la clef d’Alice ; en pratique, la toile de confiance OpenPGP est rarement utilisée, même par les « vétérans » d’OpenPGP ; la plupart des utilisateurs ont recours à d’autres canaux pour s’assurer de la validité d’une clef ;
- l’attaque est par ailleurs assez facile à détecter pour qui sait à quoi s’attendre, les clefs de taille inhabituelle (6 144 et 8 192 bits) et la présence d’un attribut utilisateur contenant une photo minuscule (262 octets) peuvent suffire à éveiller des soupçons, et dès lors un examen attentif révélera facilement la présence de la photo cachée dans le module RSA de la clef A.
La prochaine version du standard OpenPGP déconseillera formellement toute utilisation de SHA-1 dans les nouveaux messages, ce que toutes les implémentations modernes respectent déjà de toute façon.

# Je suis étonné d'être surpris...
Posté par FantastIX . Évalué à 3.
… d'après Wikipédia:
Accentuation par moi.
Alors je me demande: pourquoi?
[^] # Re: Je suis étonné d'être surpris...
Posté par gouttegd . Évalué à 10.
Pourquoi quoi ?
Pourquoi OpenPGP supporte encore SHA-1 ? Pour la même raison qu’il supporte encore 3DES, IDEA ou RIPEMD160 : parce qu’il faut gérer l’existant — notamment, tous les utilisateurs qui ont des archives d’e-mails qui remontent jusqu’aux années 2000 ou même plus loin. Et ces utilisateurs sont assez nombreux, si on en juge par les cris d’orfraie que reçoivent les développeurs de GnuPG chaque fois qu’ils évoquent la possibilité d’envisager de penser à retirer éventuellement le support d’un vieil algorithme.
Un navigateur web de 2020 peut décider de refuser de communiquer avec un serveur web utilisant des technos d’avant 2017. Une implémentation d’OpenPGP de 2020 doit être capable de lire des e-mails vieux de dix ans ou plus, sauf à mécontenter beaucoup de monde.
Pour info, ce n’est pas la première fois que seule la démonstration d’une attaque permet aux développeurs de convaincre les utilisateurs récalcitrants qu’il faut abandonner tel ou tel algorithme, que c’est un impératif de sécurité et non un caprice de développeurs. En 2018, c’est suite à la publication de l’attaque E-fail que les développeurs de GnuPG ont décidé que ce dernier refuserait désormais de déchiffrer les messages non-protégés par un code de modification d’intégrité — quelque chose qu’ils avaient déjà voulu faire plus tôt… avant de faire marche arrière suite aux plaintes d’utilisateurs qui ne pouvaient plus déchiffrer leurs archives.
Pour cette raison et quelques autres, il y a beaucoup d’inertie dans le monde OpenPGP.
[^] # Re: Je suis étonné d'être surpris...
Posté par gouttegd . Évalué à 3.
Oups, je voulais bien sûr parler d’un code de vérification d’intégrité, ou de détection de modification (Modification Detection Code ou MDC, dans le jargon du RFC4880).
[^] # Re: Je suis étonné d'être surpris...
Posté par barmic 🦦 . Évalué à 4.
Je ne remet pas en cause ce que tu dis, je me doute qu'ils ont pleins de plaintes. Mais c'est débile comme argument. Si tes mails sont si vitaux une fois reçu tu peux les déchiffrer et les rechiffrer avec l'algo de ton choix. La signature de l'émissaire ? La bonne affaire, elle était importante au moment de la réception. Tu peux ressigner toi à toi de te faire confiance que tu n'a pas altéré le message qui t'était destiné. Aujourd'hui ou dans X années, tu ne pourra de toute manière plus faire confiance en cette signature.
Encore une fois le tu représente ici celui qui joue sur une argument somme toute assez léger pour affaiblir un outil qui'il semble lui-même choisi pour sa solidité.
https://linuxfr.org/users/barmic/journaux/y-en-a-marre-de-ce-gros-troll
[^] # Re: Je suis étonné d'être surpris...
Posté par gouttegd . Évalué à 10.
Sauf qu’apparemment personne ne le fait… C’est d’ailleurs la principale raison pour laquelle la branche 1.4 de GnuPG est maintenue ad vitam aeternam : il y a beaucoup de gens qui veulent pouvoir continuer à déchiffrer des messages datant de l’époque de PGP 2.6.
Oui, ces gens feraient probablement mieux de déchiffrer ces messages une bonne fois pour toute, puis de les re-chiffrer avec une version moderne de GnuPG — pourquoi ne le font-ils pas ? Aucune idée. Peut-être qu’ils ont une excellente raison, peut-être qu’ils ont une raison débile. En attendant, c’est comme ça et il faut bien en tenir compte.
Même problème que pour le re-chiffrement. Tu peux, oui, mais en pratique ce n’est pas fait, pour une raison ou une autre.
(Un exemple de ces raisons : des experts judiciaires américains ont utilisé OpenPGP pour signer des images de disque dur, qui sont conservées dans les archives du système judiciaire US. Les plus anciennes de ces signatures n’utilisent même pas SHA-1, mais MD-5. Aucun expert n’est chaud pour demander que ces signatures soient refaites avec des algorithmes plus modernes, parce que cela pourrait entraîner la remise en question de toutes les affaires judiciaires où des signatures MD-5 ont été utilisées quelque part dans la chaîne de préservation des preuves…)
Bref, tout ça pour dire que la balance entre sécurité, utilisabilité et interopérabilité est délicate. Les développeurs OpenPGP ont généralement tendance, lorsqu’il faut arbitrer entre ces notions, à favoriser l’interopérabilité tant que la sécurité n’est pas irrémédiablement compromise, et à mon sens ils ont raison. L’alternative, c’est un système non-interopérable dans le genre de Signal, où les développeurs peuvent certes ne faire aucune concession sur la sécurité mais au prix d’un fonctionnement en vase clos qui lie les utilisateurs à un seul fournisseur.
[^] # Re: Je suis étonné d'être surpris...
Posté par barmic 🦦 . Évalué à 3. Dernière modification le 24 avril 2020 à 08:49.
Merci pour l'exemple. C'est intéressant. Je pense tout de même que le problème est que dans des cas de sécurité sur de longue période comme cela, il faudrait prévoir le maintiens de la sécurité. Comme on doit maintenir des sauvegarde (s'assurer que les disque de sauvegarde ne sont pas mort, qu'ils restent lisibles,…), il faut maintenir encore plus activement la sécurité. Ici l'absence de procédure mise en place correctement nuit gravement à la sécurité de ses données. S'ils subissent une intrusion garantir que les signatures sont intouchées sera compliqué…
Je pense que c'est compliqué. Le curseur de sécurité n'est pas évident à envisager et n'est pas forcément linéaire. En plus de ça chacun dans son contexte et de sa subjectivité a envi d'avoir un curseur positionner différemment.
Je connais mal OpenPGP, mais il doit être possible d'avoir un certain niveau par défaut et de réactiver des algo sur demande (c'est peut être ce qui est fait) ou de modulariser et d'avoir des paquets
-uglycomme le fait gstreamer ou encore de n'accepter que de lire ces algo.https://linuxfr.org/users/barmic/journaux/y-en-a-marre-de-ce-gros-troll
[^] # Re: Je suis étonné d'être surpris...
Posté par gouttegd . Évalué à 7.
Sauf que si tu essaies d’expliquer ça à un utilisateur qui demande seulement à pouvoir continuer à valider ses signatures MD-5, tu vas te prendre un retour de bâton du genre « ah, voilà bien la réponse typique d’un développeur de logiciels libres enfermé dans sa tour d’ivoire et sourd aux attentes des utilisateurs : “explique-moi quel est ton besoin, je t’expliquerai comment t’en passer” ».
C’est d’autant plus contre-productif que dans l’exemple en question, les utilisateurs en question savent bien que leur solution n’est pas sans problèmes. Ils n’ont juste pas le choix : ils ne contrôlent pas tout (comme dans beaucoup de situation, les décisions techniques ne sont pas forcément prises par ceux qui maîtrisent la technique…) et ils doivent juste faire du mieux qu’ils peuvent — alors ce n’est pas en venant leur faire des leçons que tu vas les aider.
Je n’ai pas dit le contraire.
C’est un peu tout ça à la fois qui est fait.
Au niveau du standard (en cours de refonte actuellement, même si c’est beaucoup plus long que tout le monde le souhaiterait), il est par exemple INTERDIT (MUST NOT) de générer de nouveaux messages avec MD-5, mais il est POSSIBLE (MAY) de continuer à supporter MD-5 en lecture uniquement. C’est ce qui arrivera à SHA-1 dans la prochaine version du standard.
Au niveau des implémentations, dans le cas de GnuPG :
Les trucs vraiment trop vieux sont relégués à GnuPG 1.x, dont c’est la seule raison d’être aujourd’hui ;
Dans la branche principale, les trucs qui marchent encore mais qu’on n’aime plus trop sont toujours supportés en lecture, mais utilisés en écriture seulement à la demande explicite de l’utilisateur.
Par exemple, seul GnuPG 1.x aujourd’hui peut utiliser des signatures MD-5, GnuPG 2.2 les refuse complètement, même en lecture. Dans le cas de SHA-1, jusqu’à ces derniers mois il n’était plus utilisé par défaut (depuis 2009) mais était toujours utilisable sur demande, et accepté en lecture sauf demande contraire (option
--weak-digest-algo SHA1) ; depuis la publication de cette attaque, il n’est plus accepté même en lecture.[^] # Re: Je suis étonné d'être surpris...
Posté par FantastIX . Évalué à 9.
Voilà.
Merci beaucoup. Cette explication m'a définitivement fait comprendre. Je m'aperçois que je n'avais qu'une vue parcellaire de OpenPGP et ce qui me paraissait évident ne l'était que parce que je n'avais pas connaissance du contexte global. Merci pour ton explication, au moins c'est limpide, maintenant.
# SHA-1 c'est nul. Utilisez MD5
Posté par xryl669 . Évalué à 1.
MD5, c'est le futur, c'est rapide, peut être pas autant qu'un bon CRC-32, mais bon, il faut quand même que l'ordinateur rame un peu lorsqu'il signe un very important mail sinon l'utilisateur pensera que c'est bidon le cryptage.
[^] # Re: SHA-1 c'est nul. Utilisez MD5
Posté par Colin Pitrat (site web personnel) . Évalué à 2.
MD4 était plus performant. Est-ce du bloatware ou de l'obsolescence programmée ? Incompétence ou complot intergalactique ? Toujours est-il que les nouvelles versions sont systématiquement plus gourmandes que les anciennes.
[^] # Re: SHA-1 c'est nul. Utilisez MD5
Posté par Serge Julien . Évalué à 7.
MD5 c'est has been!
Un bon vieux bit de parité te permet d'être certain·e que ton message n'a pas été altéré.
Et c'est imbattable pour ce qui est de la vitesse de calcul!
# C'était pourtant logique
Posté par Pol' uX (site web personnel) . Évalué à 9.
Avec un hash qu'est naze, on pouvait s'attendre à des données cacher.
Adhérer à l'April, ça vous tente ?
# On propose quoi ?
Posté par Charly.the.daemon . Évalué à 0.
À quand un ECC en guise de signature ?
Ça ne me semble pas déconnant au premier abord ?
[^] # Re: On propose quoi ?
Posté par gouttegd . Évalué à 8.
?
Les signatures utilisant la cryptographie sur courbes elliptiques (ECC), ça fait déjà plusieurs années que c’est possible. C’est standardisé pour OpenPGP depuis le RFC 6637, et GnuPG supporte ça depuis la version 2.1 — et à ma connaissance la plupart des autres implémentations le supportent aussi.
Mais des signatures ECC ne changeraient rien ici. Le choix de l’algorithme de signature (RSA, DSA, ECDSA ou EdDSA) est orthogonal au choix de l’algorithme de condensation (SHA-1, RIPEMD-160, SHA2-256, etc.), qui est appliqué sur le document à signer avant la signature proprement dite (c’est le résultat de cette opération de condensation qui est donné en entrée à l’algorithme de signature).
Il est parfaitement possible (bien qu’aucune implémentation ne le fasse par défaut, ça doit être explicitement configuré par l’utilisateur) de condenser avec SHA-1 et de signer ensuite avec une clef ECDSA ou EdDSA. L’attaque rapportée ici fonctionnerait tout aussi bien que dans le cas où c’est RSA qui est utilisé pour signer.
(Tout au plus, une signature faite avec SHA-1 + ECDSA éveillerait davantage de soupçons qu’une signature SHA-1 + RSA, parce que toutes les implémentations supportant ECDSA supportent aussi SHA-2 et l’utilisation de SHA-1 serait donc « surprenante » dans ce contexte — alors qu’on peut penser qu’une signature RSA a été émise par une implémentation plus ancienne ne supportant pas SHA-2.)
# Et après on fait quoi ?
Posté par G.bleu (site web personnel) . Évalué à 4.
De ce que j'ai compris, une fois cette attaque réussie on se retrouve avec une clé publique B apparaissant comme appartenant a Alice et certifiée par Charlie.
Par contre la clé B en question a été créée de façon spécifique à l'attaque (notamment le fait de devoir contenir un fichier JPEG valide ainsi que le user id de alice à sa fin).
Du coup on ne dispose pas de la partie privée de cette clé, et la retrouver revient à essayer de retrouver la vrai clé privée de Alice à partir de sa clé publique…
Bref je ne vois pas l'utilité pratique de cette attaque (mais c'est malgré tout du très beau travail hein ! ), j'ai raté un truc ?
[^] # Re: Et après on fait quoi ?
Posté par gouttegd . Évalué à 5.
Si. :) Mais j’ai simplifié l’explication de l’attaque en laissant de côté certains aspects.
Notamment, dans la clef A, l’espace visible entre le marqueur de fin d’image JPEG (le trait rouge sur le schéma à la fin du journal) et la fin du paquet de clef publique qui le contient est utilisé pour générer un module et un exposant public RSA valide, correspondant à un exposant privé calculé par ailleurs.
Similairement, dans la clef B, il y a un peu d’espace entre l’endroit où la collision est établie et la fin du paquet de clef publique — là encore, on joue sur ces octets pour faire en sorte que le paquet contienne au bout du compte une clef publique valide, correspondant à une clef privée calculée par ailleurs.
À l’arrivée, Mallory possède bien deux clefs OpenPGP « complètes » (parties publiques et privées) — dont une semblant appartenir à Alice, appartenance confirmée par la signature de Charlie.
[^] # Re: Et après on fait quoi ?
Posté par G.bleu (site web personnel) . Évalué à 1.
Merci pour ces explication, et j'en profite pour te féliciter pour ton article qui a été un vrai plaisir à lire ;-)
# SHA-perlipopette
Posté par Bastoon . Évalué à 0.
SHA, SHA2-mande à faire attention SHA-que fois qu'on ajoute une clé.
Suivre le flux des commentaires
Note : les commentaires appartiennent à celles et ceux qui les ont postés. Nous n’en sommes pas responsables.