Journal La recherche en langages de programmation au quotidien

Posté par  . Licence CC By‑SA.
Étiquettes :
81
6
fév.
2018

Sommaire

Dans le cadre de mon travail j'ai été amené à écrire un petit texte qui explique mon quotidien fait de "recherche (scientifique) en langages de programmation". Je me permets de le diffuser ici au cas où ça intéresse des gens.

Ma recherche

Je travaille à l'INRIA, un institut public français de recherche en informatique. Je fais de la programmation et de la recherche sur les langages de programmation.

Mon rôle est d’étudier ces langages, de mieux les comprendre, pour identifier les propriétés désirables et capturer des éléments de langage qui sont les plus simples, performants et sûrs à utiliser. Cela permet faire évoluer les langages déjà existants, voire même de créer un langage où il est plus facile de dire à la machine ce que l’on veut qu’elle fasse, et où la machine est aussi mieux capable de vérifier que notre demande est cohérente.

(Pour plus d'information sur l'étude mathématique des langages de programmation, voir mon précédent journal Pourquoi la recherche en langages de programmation ?.)

Ma recherche est aussi liée au développement des assistants de preuve, des outils qui permettent non pas d’écrire des programmes et de les faire faire exécuter par l’ordinateur, mais d’écrire des preuves mathématiques et de les faire vérifier par l’ordinateur. L’interaction entre langages de programmation et assistants de preuves est double. D’une part, beaucoup de travaux sur les langages de programmation peuvent être réutilisés pour comprendre les « langages de preuve » des assistants de preuve. D’autre part, nous essayons de concevoir des langages dans lesquels on puisse donner une spécification du comportement de son programme, et aider ensuite l’ordinateur à vérifier, à prouver que la spécification est vérifiée par le programme – ces langages intègrent donc des outils de recherche de preuve et d’assistance à la preuve.

L'équipe de recherche dans laquelle je travaille, nommée Parsifal, étudie la théorie de la démonstration, c'est-à-dire l’étude formelle des preuves mathématiques. Certains mathématiciens étudient les nombres, les événements aléatoires ou les surfaces géométriques, nous étudions les preuves mathématiques elles-mêmes comme des objets formels. C’est un sujet essentiel pour comprendre la recherche de preuve, les assistants de preuve, mais qui a aussi des applications nombreuses pour étudier les langages de programmation : en regardant d’une certaine façon peut voir qu’un « programme » est aussi une « preuve » et inversement. J’utilise cette correspondance preuves-programmes dans mon travail et j’espère continuer à la développer.

Mon quotidien

Au jour le jour, ma façon de travailler ressemble à celle des mathématiciens et mathématiciennes : j’essaie de comprendre quels résultats je veux établir, et ensuite comment les prouver. Un article scientifique dans mon domaine commence typiquement par expliquer un problème perçu dans un langage de programmation donné, une proposition de solution, puis donner une définition mathématique du langage corrigé, et montrer un théorème qui nous convainc que le problème n’est plus présent. Souvent, on ne travaille pas sur un langage existant en entier, mais sur une version simplifiée, conçue pour garder uniquement les aspects que nous souhaitons étudier.

Bref, je peux présenter mon travail de recherche avec des définitions, des lemmes et des théorèmes. Mais souvent je vais aussi essayer d’implémenter les langages et les programmes considérés, pour pouvoir exécuter des exemples sur un ordinateur, comprendre certaines propriétés de l’exécution, et aussi garder un lien de praticien avec l’activité de programmation que j’étudie.

Concrètement, vous pouvez voir sur les images ci-dessous à quoi ressemble une session de travail sur Abella, un nouvel assistant de preuve en cours de développement au sein de l’équipe Parsifal. On voit à gauche une zone bleue qui représente la partie déjà vérifiée par l'outil (les preuves dans cette partie sont correctes), une zone noire qui n'a pas encore été vérifiée (on est en train d'écrire la preuve), et à droite on voit le "but" courant, ce qu'il reste à faire vérifier pour conclure la preuve :

une interface d'assistant de preuve

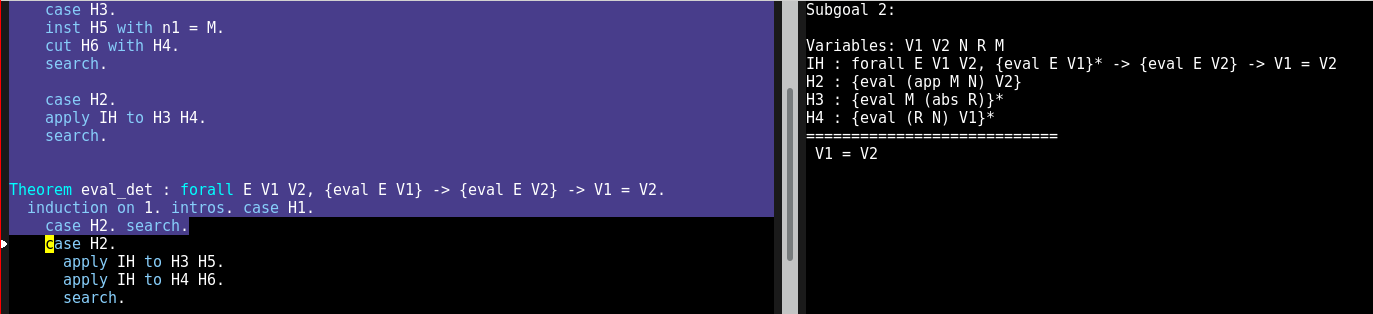
Les assistants de preuve ont vocation à être utilisés par tous les scientifiques faisant des raisonnement mathématiques, mais il reste du travail pour qu’ils soient plus faciles à utiliser—ils sont aujourd'hui réservés aux spécialistes du domaine. Ma communauté de recherche fait des efforts pour adopter ces outils, je m’en sers parfois pour valider mon propre travail, et cela permet de découvrir des problèmes d’utilisation, des points à améliorer pour pouvoir espérer une adoption plus grande. Aujourd’hui quand quelqu’un annonce un nouveau résultat mathématique, il peut être très difficile de savoir si le résultat est correct ou non ; il sera peut-être un jour réaliste de demander à la personne de fournir une preuve vérifiée par un assistant de preuve, pour accélérer son étude et sa compréhension par les scientifiques du domaine.

Échanger avec l’extérieur

De nouveaux langages de programmation apparaissent tous les ans. Une partie est construite par des scientifiques du domaine, ou des gens qui ont étudié notre travail, mais la majorité vient de personnes spécialistes d’un tout autre domaine de la programmation, qui veulent créer un bon langage pour leurs besoins, sans avoir étudié la théorie.

Une partie de notre travail consiste donc à entrer en contact avec les personnes qui créent de nouveaux langages et les utilisent, pour leur transmettre de bonnes pratiques de conception, les alerter sur des problèmes à venir, et aussi découvrir de leurs besoins et idées pour faire évoluer notre compréhension commune des langages de programmation. Nous avons parfois des discussions directes avec l’équipe qui conçoit un langage, et il nous arrive même de travailler scientifiquement sur ces nouveaux langages (récemment ma communauté s’est penchée sur les langages R, Ceylon, Rust et Julia par exemple), mais nous avons aussi un impact indirect, en faisant utiliser des langages conçus par notre communauté dont certaines idées inspirent ensuite les nouveaux langages de programmation. Étudier les nouveaux langages de non-spécialistes nous permet aussi de découvrir de nouveaux besoins qui viennent enrichir notre activité de recherche.

Ainsi, je travaille sur le langage de programmation OCaml (comme scientifique et aussi comme contributeur et co-mainteneur de l’implémentation), conçu à l'INRIA et encore développé en grande partie dans l’institut. Le langage est utilisé dans des projets venant de tous les horizons, la recherche, le logiciel libre et l’industrie, qui font connaître ses idées à un public plus large. L’idée de programmation « fonctionnelle », mettant l’accent sur l’importance de raisonner rigoureusement sur son code, est promue par OCaml mais aussi d’autres langages comme Scala, Haskell, ou le langage F# (dérivé de OCaml), et influence les évolutions de langages grand public comme Java, C# ou Javascript.

un exemple de code OCaml

Recherche et logiciel libre

Les résultats de mes travaux sont accessibles à tous—pour moi c'est une part essentielle du contrat moral de la recherche publique. Mes publications sont en accès libre (et archivées sur arXiv et/ou HAL (si possible en licence CC-BY, mais malheureusement ce n'est pas toujours moi qui décide), et le logiciel produit est sous licence libre.

Dans le cadre de mon activité de recherche, je produis surtout des petits prototypes qui ne sont pas forcément très intéressants pour les autres—même s'il m'arrive de partager effectivement du code avec d'autres chercheurs ou de collaborer sur leurs projets. Mon activité de développement principale tourne autour de l'implémentation du langage OCaml, et d'outils et bibliothèques de son écosystème (je travaille là-dessus dans une zone assez floue entre le temps libre/personnel et le temps de travail).

Le compilateur OCaml est un logiciel libre, et j'essaie (ainsi que les autres mainteneurs) de faire des efforts pour encourager les contributions externes—faire des revues de code pour les contributeurs externes, marquer des bugs comme "faciles" sur le bugtracker, organiser des réunions d'initiation à la contribution.

Un langage de programmation qui a des utilisateurs n'est pas un projet libre facile à gérer : il faut être très prudent quand on accepte de nouvelles fonctionnalités pour préserver la compatibilité arrière et éviter l'enfouissement sous les fonctionnalités (feature bloat). Du coup il peut être très difficile de juger des propositions de changement et de prendre des décisions, ce qui frustre les contributeurs. Une nouvelle fonctionnalité peut attendre dans un coin pendant des années parce qu'elle n'est "pas complète", voire même parce qu'il y a deux propositions de syntaxe différentes et qu'on ne sait pas laquelle on préfère. Ce n'est pas unique à OCaml; tout langage est beaucoup plus difficile à évoluer qu'il n'y paraît au premier abord. C'est une raison de plus de bien faire attention à la théorie quand on conçoit un langage ou une nouvelle fonctionnalité, pour essayer d'avoir la meilleure première version possible :-)

Ces derniers temps j'ai aussi eu l'occasion de faire un peu de gestion des publications de nouvelle version (release management), à l'occasion en particulier d'un congé parental pris par le gestionnaire de nouvelles versions habituel, Damien Doligez. Le plus difficile dans cette partie du travail est de décider comment réagir en cas de problème repéré tard dans le cycle de développement, et d'évaluer la sûreté et les risques pour la compatibilité arrière des correctifs proposés—un correctif risque toujours d'introduire de nouveaux problèmes.

  • # c'est bien joli, mais…

    Posté par  . Évalué à 2.

    je travaille à l'INRIA

    tu veux dire Inria? ^^

    The cake is a lie.

    • [^] # Re: c'est bien joli, mais…

      Posté par  . Évalué à 5.

      tu veux dire Inria? ^

      C'est une boutade au sein de l'Institut depuis qu'ils ont changé leur identité visuelle ?

      En tout cas, gasche suit la graphie de sa nouvelle équipe — qui n'a peut être pas mis à jour sa page de présentation depuis le changement, à la lecture des dates qui y figurent.

      Sapere aude ! Aie le courage de te servir de ton propre entendement. Voilà la devise des Lumières.

      • [^] # Re: c'est bien joli, mais…

        Posté par  (site web personnel) . Évalué à 5.

        Il faut dire que ces changements de graphie sont débiles. J'invite tout le monde à prendre le "nouveau" logo du CNRS en miroir vertical… Bref, c'est de l'argent du contribuable vraiment mal dépensé.

        • [^] # Re: c'est bien joli, mais…

          Posté par  . Évalué à 10.

          Note pour moi-même : ne pas faire cet essai au taf avec un Zippo quand on n'a pas de mirroir :
          1- On passe pour un con à coller son Zippo contre l'écran.
          2- On explique pourquoi on fait ça et on montre que cnrs ça fait culs en miroir vertical, on repasse pour un con.

          La majeure partie des morts l'était déjà de son vivant et le jour venu, ils n'ont pas senti la différence.

          • [^] # Re: c'est bien joli, mais…

            Posté par  (site web personnel) . Évalué à 7.

            Pour ceux qui n'ont pas de zippo ou de miroir:

            cnrs inversé

            Dans Gimp: sélection de la zone, outil, transformation, retourner.

            Ça me fait penser au logo TGV qui est un escargot à l'envers.

      • [^] # Re: c'est bien joli, mais…

        Posté par  . Évalué à 3.

        En tout cas, ils ont financé et publié une fonte libre pour leur identité visuelle et ça c'est quand même pas mal du tout.

    • [^] # Re: c'est bien joli, mais…

      Posté par  . Évalué à 3.

      Étonnant ce moinssage car tu as raison, sur leur propre site la graphie est bien « Inria ».

      Je l’aurais moi aussi écrit en majuscule, c’est bien un sigle, c’est étrange de l’écrire en minuscules…

      • [^] # Re: c'est bien joli, mais…

        Posté par  . Évalué à 6.

        Nope, ça se prononce donc c’est non seulement un sigle mais c’est aussi un acronyme : https://fr.wikipedia.org/wiki/Acronymie

        et un acronyme peut s’écrire comme un nom propre d’après la page que je lie.

        • [^] # Re: c'est bien joli, mais…

          Posté par  . Évalué à 2.

          que je lie.

          Je savais bien qu'il y avait un lien entre les acronymes et les sigles!

      • [^] # Re: c'est bien joli, mais…

        Posté par  (site web personnel) . Évalué à 2.

        C'est surtout qu'il sont passés d'un acronyme INRIA à une vrai nom, comme une marque. Ce n'est plus l'INRIA, mais Inria.

        • [^] # Re: c'est bien joli, mais…

          Posté par  . Évalué à 7.

          Ça c'est la volonté de leur service de communication. Légalement leur nom c'est toujours l'« institut national de recherche en informatique et en automatique », décret qui porte organisation de l'INRIA, et aussi par exemple un arrêté récent du JO qui parle de l'INRIA.

          Bref, l'institut veut se faire appeler Inria et pas l'INRIA, que les membres disent « je suis à Inria » et non « je suis à l'INRIA », mais ça ce n'est qu'une lubie de l'institut et ça ne change pas son nom qui est Institut National de Recherche en Informatique et en Automatique.

          En plus vouloir l'utiliser sans le « l' » conduit à un hiatus qui apparaît d'autant plus injustifié que le nom de l'institut n'a pas changé.

        • [^] # Re: c'est bien joli, mais…

          Posté par  . Évalué à 3.

          OK, et bien tu me l’apprends… Je ne vois pas l’utilité, j’aime les sigles (et acronymes). Ça ne veut rien dire en tant que mot. On va me dire, un nom de marque n’a pas forcément à signifier quelque chose mais je continue de trouver ça nul… La plupart des marques qui ne sont pas des sigles/acronymes ont une signification précise (en rapport avec la ville d’origine, ou le nom des fondateurs ou fondatrices, ou la raison d’être de la société, etc…)

          Quelle est la raison invoquée pour passer de INRIA à Inria ? Est-ce pour entériner un usage courant ? Ou bien pour montrer qu’on se modernise ou autre chose ?

          • [^] # Re: c'est bien joli, mais…

            Posté par  (site web personnel) . Évalué à 5. Dernière modification le 07 février 2018 à 18:26.

            Quelle est la raison invoquée pour passer de INRIA à Inria ? Est-ce pour entériner un usage courant ? Ou bien pour montrer qu’on se modernise ou autre chose ?

            C'est comme pour le CNRS et plein d'organisme… Il y a une pseudo mode anti-moderne qui a décrété que l'écriture de type 'Marque' était bien plus "hype" et que les majuscules étaient "hass been"… Tout cela coûte très cher et n'a absolument aucun intérêt mais les services com recrutent et tournent à plein régime !

  • # Passionant

    Posté par  (site web personnel) . Évalué à 10.

    Merci à toi de partager quelques instants de ton quotidien avec nous, de démystifier l'activité de recherche et montrer à quoi « ça sert » puisque l'on vit dans un monde où la finalité semble importante à beaucoup :-/

    Quelques questions ! Tu dis que ta communauté est en contact avec celle qui poussent des langages comme Julia. Concrètement, comment se passent vos échanges, sur quels types de questions vous penchez vous etc ? Êtes-vous en contact avec la communauté LLVM pour aller vers des transformations prouvées, faire évoluer l'IR etc ?

    Et tu n'as pas parlé d'une partie qui me semble prendre de plus en plus de temps dans le monde académique : la recherche de financement. Est-ce parce que l'INRIA est protecteur de ce point de vue, parce que c'est une partie négligeable dans ton cas, autre ?

    Encore merci pour l'effort de vulgarisation et de partage !

    • [^] # Re: Passionant

      Posté par  . Évalué à 6.

      J'abonde dans le même sens : ce témoignage est super intéressant :)

      BeOS le faisait il y a 20 ans !

    • [^] # Re: Passionant

      Posté par  . Évalué à 7. Dernière modification le 07 février 2018 à 11:47.

      Et tu n'as pas parlé d'une partie qui me semble prendre de plus en plus de temps dans le monde académique : la recherche de financement.

      Pour le langage développé au sein de sa nouvelle équipe, on trouve ces informations sur le site du langage. À l'origine, le projet fut financé par l'entreprise Boston Scientific spécialisé dans le matériel médical, puis par des fonds publics provenant de la National Science Foundation (équivalent américain du CNRS).

      Je me demande, d'ailleurs, si le nom du langage (Abella) ne vient pas du premier financeur : l'entreprise a été cofondée par John Abele. Au départ (j'aime bien essayé de trouver l'origine des noms des projets) je pensais que le nom faisait référence au logicien de l'époque scolastique Pierre Abélard car il est souvent utilisé en théorie de la démonstration avec sa bien aimée Héloïse (comme dans l'article Formules valides, jeux et protocoles réseau qui utilise des principes identiques à ceux dont parle gasche dans son journal, mais pour la certification de protocoles réseau), mais l'hypothèse de John Abele me semble plus probable.

      démystifier l'activité de recherche et montrer à quoi « ça sert » puisque l'on vit dans un monde où la finalité semble importante à beaucoup :-/

      Il en a été de tout temps ainsi, et une citation du maître pour la route :-)

      Il n'est point de connaissance qui soit superflue et inutile de façon absolue et à tous égards, encore que nous ne soyons pas toujours à même d'en apercevoir l'utilité. C'est par conséquent un objection aussi mal avisée qu'injuste que les esprits superficiels adressent aux grands hommes qui consacrent aux sciences des soins laborieux lorsqu'ils viennent demander : à quoi cela sert-il ? On ne doit en aucun cas poser une telle question quand on prétend s'occuper de science. À supposer qu'une science ne puisse apporter d'explication que sur un quelconque objet possible, de ce seul fait son utilité serait déjà suffisante. Toute connaissance logiquement parfaite a déjà quelque utilité possible : même si elle nous échappe jusqu'à présent, il se peut que la postérité la découvre. Si en cultivant les sciences on n'avait jamais mesuré l'utilité qu'au profit matériel qu'on pourrait retirer, nous n'aurions pas l'arithmétique et la géométrie. Aussi bien notre intelligence est ainsi conformée qu'elle trouve satisfaction dans la simple connaissance, et même une satisfaction plus grande que dans l'utilité qui en résulte. Platon l'avait déjà remarqué. L'homme y prend conscience de sa valeur propre; il a la sensation de ce qui se nomme : avoir l'intelligence. Les hommes qui ne sentent pas cela doivent envier les bêtes. La valeur intrinsèque que les connaissances tiennent de leur perfection logique est incomparable avec leur valeur extrinsèque, qu'elles tirent de leur application.

      Emmanuel Kant, Logique

      Sapere aude ! Aie le courage de te servir de ton propre entendement. Voilà la devise des Lumières.

    • [^] # Re: Passionant

      Posté par  . Évalué à 8.

      Et tu n'as pas parlé d'une partie qui me semble prendre de plus en plus de temps dans le monde académique : la recherche de financement. Est-ce parce que l'INRIA est protecteur de ce point de vue, parce que c'est une partie négligeable dans ton cas, autre ?

      Je suis jeune chercheur; je n'ai pas encore cherché à encadrer des étudiants pour un stage rémunéré ou surtout une thèse, donc je n'ai pas eu de besoin direct de financement. C'est quelque chose que je découvrirai dans les années à venir.

      Mes seules sources de dépenses pour l'instant (à part le salaire) sont les voyages. Je voyage pas mal dans le cadre de mon travail (pour rendre visite à des équipes de recherche à qui expliquer mon travail, assister à des conférences internationales, etc.). L'INRIA fournit à mon équipe un budget pour cela, et je suis relativement bien loti. Pour 2018 je peux dépenser environ 3000€ en voyages, ce qui convient si on est raisonnable; c'est plus que d'autres collègues en France (ou encore plus qu'en Amérique du Sud, en Grèce, etc.), mais moins que les gens qui ont obtenu des financements complémentaires. En comparaison, une conférence d'une semaine aux États-Unis au moins $2200.

      Tu dis que ta communauté est en contact avec celle qui poussent des langages comme Julia. Concrètement, comment se passent vos échanges, sur quels types de questions vous penchez vous etc ? Êtes-vous en contact avec la communauté LLVM pour aller vers des transformations prouvées, faire évoluer l'IR etc ?

      J'ai des collègues qui ont travaillé sur le fait de comprendre la relation de "sous-typage" de Julia (voir ce résumé d'exposé), qui est utilisée pour résoudre les appels de fonction (multi-method dispatch). Cette relation était définie assez vaguement dans la documentation, et il y a une implémentation de référence qui est compliquée (c'est une partie qui a évolué avec le temps et pleine d'optimisations variées). Ils et elles ont trouvé des aspects non-intuitifs de cette implémentation, certains qui sont des bugs qui ont été corrigés par les implémenteurs du langage, certains qui sont des difficultés de conception qui demanderaient des évolutions du langage, ou à prendre en compte pour un nouveau langage de ce genre. Les discussions se font souvent par email, parfois en direct (une partie de ces collègues est à Boston, et une partie des développeurs Julia aussi), et portent sur des questions précises (tel comportement est-il intentionnel ou bien un bug ?) ou sur des questions plus générales (voici comment on comprend/modélise ceci ou cela, est-ce que ça correspond à votre intuition / votre implémentation ?). Ce n'est pas toujours évident de discuter parce que les connaissances de chacun peuvent être très différentes—les développeurs de Julia ne connaissent pas forcément bien le typage, même si leur langage l'utilise en fait de façon fondamentale.

      Êtes-vous en contact avec la communauté LLVM pour aller vers des transformations prouvées

      Oui, voir par exemple Provably Correct Peephole Optimizations with Alive, Nuno P. Lopes, David Menendez, Santosh Nagarakatte et John Regehr, 2015.

      (Techniquement ces chercheurs sont dans une communauté un petit plus éloignée de la mienne, plus orientée "compilation" et "vérification automatique" que "sémantique des langages de programmation" et "typage"—mais ce sont des proches qui discutent beaucoup ensemble.)

      Ce n'est pas facile parce que les développeurs de LLVM s'intéressent peu aux méthodes formelles et, en général, à la correction de leurs passes (l'idée d'ensemble est que si ça passe dans la testsuite, c'est raisonnable), mais il y a eu un gros travail de discussion/sensibilisation sur ces dernières années (un des chercheurs sur ce travail, Nuno Lopes, contribute maintenant régulièrement au code, et ça aide), donc ça progresse petit à petit.

      faire évoluer l'IR (LLVM) etc ?

      Oui, Taming Undefined Behavior in LLVM, Juneyoung Lee, Yoonseung Kim, Youngju Song, Chung-Kil Hur, Sanjoy Das, David Majnemer, John Regehr, Nuno P. Lopes, 2017.

  • # Lisibilité

    Posté par  . Évalué à 9. Dernière modification le 07 février 2018 à 12:18.

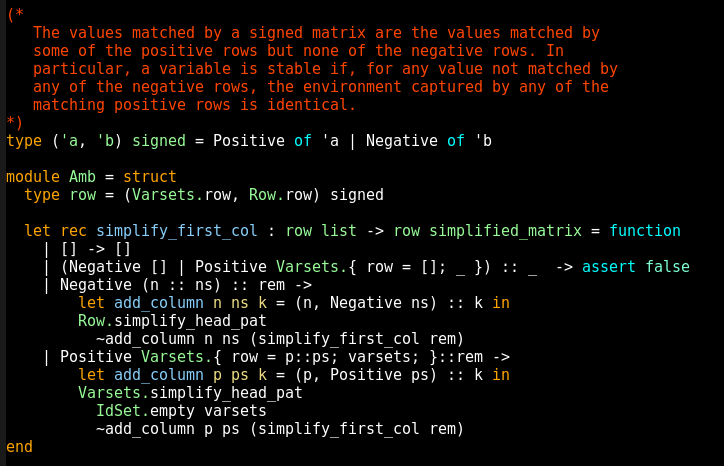
    Pardon pour les puristes et les adorateurs de langages fonctionnels abscons mais quand je vois un truc comme ça :

    .{ row = []; _ }) :: _ -> asset

    Je me dis : "Mais c'est du Brainfuck bien sûr !"

    • [^] # Re: Lisibilité

      Posté par  . Évalué à 9.

      La grande majorité des langages de programmation permettent d'écrire des choses que quelqu'un qui ne connaît pas le langage trouvera difficile à lire. (Ceux qui ne le permettent pas sont jugés trop verbeux.). Je ne pense pas que cet exemple montre que OCaml est plus "abscons" qu'un autre langage dans l'absolu, mais plutôt que tu n'es pas déjà habitué à sa syntaxe.

      En l'occurrence, il s'agit d'un filtrage de motif:

      • { row = []; _ } est un motif qui teste si la valeur observée est un bien un enregistrement ({ ... }) (record en OCaml, un type produit avec des champs nommés, comme une struct en C) avec un champ row contenant la liste vide (row = []) et potentiellement d'autres champs ; _. Il se trouve que ce record est défini dans le module Varsets, d'où le Varsets. pour qualifier.
      • (Negative [] | Positive Varsets.{ row = []; _ }) est un motif qui filtre une entrée de type (Varsets.row, Row.row) signed, c'est-à-dire soit une valeur de la forme Positive foo où foo est une liste (c'est la définition de Row.row), ou une valeur de la forme Negative bar où bar est de type Varsets.row (l'enregistrement). Ce motif-ci accepte soit la liste vide dans le cas Negative, soit un Varsets.row dont le champ row est la liste vide dans le cas Positive — donc une ligne vide, qu'elle soit positive ou négative.
      • (Negative [] | Positive Varsets.{ row = []; _ }) :: _ est un motif de liste (p :: q filtre une liste chaînée dont le premier élément filtre p et la suite filtre q), qui filtre une liste dont le premier élément est une ligne vide (positive ou négative), et la suite n'importe pas.

      La ligne de code complète dit donc que si on prend en entrée une matrice dont la première ligne est vide (positive ou négative), alors on fait un assert false: cette fonction ne doit être appelée que sur des matrices dont la première ligne est non-vide. Les clauses suivantes du filtrages vont donc pouvoir gérer le cas où la première colonne est négative non-vide (Negative (n :: ns)) ou positive non-vide (Positive Varsets.{ row = p::ps; varsets; }).

    • [^] # Re: Lisibilité

      Posté par  . Évalué à 5.

      Pardon pour les puristes

      Les puristes de quoi ? et si on est un adorateur de langage fonctionnel pas abscons tu t’excuses pas ? Pas très rigoureux tout ça ;)

  • # mon préféré: python

    Posté par  (site web personnel) . Évalué à 2.

    Quel est ton avis sur mon langage préféré: python auquel je n'ai pas fait défaut depuis sa découverte il y a une dizaine d'année ?

    • [^] # Re: mon préféré: python

      Posté par  . Évalué à 10.

      C'est un peu hors-sujet alors j'ai créé un topic ailleurs pour en discuter: De la conception du langage Python.

      • [^] # Re: mon préféré: R

        Posté par  (site web personnel, Mastodon) . Évalué à 6.

        Pardon d’avance si je transforme les commentaires de ce journal en « ask me anything ». Mais comme j’ai apprécié lire ton journal et tes commentaires sur Python, maintenant j’ai envie de poser la même question pour R que tu as aussi évoqué. :-)

        Pour mettre les choses en contexte : je suis biochimiste de formation, on ne m’a jamais proposé de programmation dans mon cursus (à part 2 mois de Matlab, mais ça consistait surtout à adapter des codes fournis par le prof…). Au début j’ai commencé par bricoler un peu avec Python, principalement par curiosité (en essayant de résoudre les problèmes de http://rosalind.info ; c’était quand j’avais besoin de me changer les idées pendant la rédaction de ma thèse…), mais comme je n’avais pas de projet concret je m’en suis lassé assez rapidement.

        Maintenant je m’y intéresse bien plus, parce que dans mon travail au quotidien ça m’aide à résoudre des problèmes conceptuellement simples mais affreusement pénibles à traiter manuellement. L'année dernière, je me suis mis à R cette fois pour résoudre un problème concret de mon quotidien (qui était faisable dans un tableur pour un jeu de données, mais devenait ultra-pénible dès qu’il fallait le faire 2 fois de suite ou plus comme c’était systématiquement le cas). Cette expérience a été bien plus amusante, en particulier j’ai trouvé très satisfaisant de créer mes propres outils. J’ai aussi eu l’impression que R essayait beaucoup moins de me mettre des bâtons dans les roues (dit autrement, j’arrivais plus facilement à mon but).

        Je suppose que mes expériences avec ces deux langages diffèrent beaucoup principalement du fait d’avoir eu ou pas un projet concret sur lequel les appliquer. Mais je suis tout de même intéressé de comprendre s’il y a des raisons plus profondes dues à la conception des deux langages qui pourraient aussi en partie expliquer ces expériences différentes.

        • [^] # Re: mon préféré: R

          Posté par  . Évalué à 6.

          À mon avis, R est un langage très très pratique. On peut l'utiliser dans le but premier pour lequel il a été conçu (ouvrir un terminal et faire une analyse statistique et graphique d'un jeu de données), mais il est également très pratique pour écrire des simulations, manipuler des fichiers de données, etc. On peut facilement le scripter, et il embarque nativement un pré-compilateur et des fonctions de parallélisation.

          Sa force principale, c'est son écosystème. Il est possible de trouver des paquets tout faits et de tutoriels pour une multitude de trucs en biologie, statistiques, bio-informatique, etc. Ça peut vraiment faire gagner un temps fou.

          Par contre, ce n'est quand même pas un langage très "beau". C'est un langage fonctionnel en théorie, mais en pratique, il est multiparadigme ; rien n'est vérifié (pas de typage, pas de vérification des entrées/sorties des fonction, les erreurs se progagent très loin et finissent par ressortir des messages cryptiques dans des fonctions internes…), il existe deux implémentations totalement différentes d'un début de fonctionnement orienté objet (classes S3 et classes S4), issues de ce que je considère comme un manque flagrant de volonté de décider (ça crée des "dialectes" du langage qui sont incompatibles). Idem pour les namespace ou les systèmes de paquets, qui sont complexes à gérer et à comprendre, et qui, au final, ne résolvent pas vraiment le problème du passage aux gros projets. Le langage n'est pas très homogènes (noms de paramètres différents dans les classes de base, par exemple) du fait de l'évolution du langage (intégration progressive des fonctions les plus courantes dans le namespace "base").

          Bref, R est un super outil, j'aime beaucoup ce langage, mais je pense que s'il était à refaire, les choix devraient nécessairement être différents, parce que la situation actuelle est un peu bordélique.

      • [^] # Re: mon détesté: java

        Posté par  . Évalué à -1.

        Quel est ton avis sur mon langage détesté: java auquel j'ai fait défaut depuis sa découverte il y a une dizaine d'année ?

        Dire que vous vous n'en avez rien à faire de la vie privée parce que vous n'avez rien à cacher, c'est comme dire que vous n'en avez rien à faire de la liberté d'expression parce que vous n'avez rien à dire. Edward Snowden

    • [^] # Re: mon préféré: python

      Posté par  (site web personnel) . Évalué à 2.

      Au fait, je me suis toujours demandé si tu avais un rapport avec l'ami Christophe Combelle, éminent pythoniste français — qu'on voit moins souvent par ici d'ailleurs.

      "La liberté est à l'homme ce que les ailes sont à l'oiseau" Jean-Pierre Rosnay

  • # Perl6

    Posté par  (site web personnel) . Évalué à 5.

    L'INRIA travaille et étudie pleins de langages de programmation et pourtant, j'ai l'impression que l'institut n'a jamais investi dans le langage Perl6.

    Or si on regarde la conception de ce langage et son implémentation actuelle, c'est un langage tellement riche que je ne comprends pas pourquoi l'INRIA ne semble pas avoir ni vouloir jouer avec.

    • [^] # Re: Perl6

      Posté par  . Évalué à 4.

      Je pense (cela ne regarde que moi) que L'INRIA s'intéresse plus à (je cite l'OP) un langage "où la machine est mieux capable de vérifier que notre demande est cohérente", qu'à un langage "où il est plus facile de dire à la machine ce que l’on veut qu’elle fasse".
      Perl6 rentre dans le deuxième cas. De plus la vérification mathématique des E/S que cible l'OP, n'est possible qu'à travers le parser NPQ de perl6.

      On entre alors dans la vérification majoritairement syntaxique (préfixes, suffixes, priorités, etc…), voire linguistique de la cohérence avec ses règles internes; qu'à une sortie "pure" du point de vue mathématique.

      C'est toujours le même débat sur Perl* revenant à l'illisibilité du code, qui de façon 'inconsciente' le rend non viable car visiblement chaotique. Pour ce qui est de perl6, sa syntaxe a fait de grands progrès de cohérence et le rend idéal pour un premier langage d'apprentissage.

      Préférer l'utilisateur à la machine reste pour moi un critère majeur dans l'appréciation d'un langage informatique, et perl6 réussit bien ce pari.

      Afin de ne pas me faire "moinsser", je souligne (encore) que ce n'est que mon point de vue.

      • [^] # Re: Perl6

        Posté par  (site web personnel) . Évalué à 4.

        Je te rassure, je n'utilise quasiment JAMAIS le + et le -… Je me souviens qu'à l'époque d’Eiffel, l'INRIA a poussé a un clone du langage plutôt que de suivre la voie bien plus intéressante à mon avis de Sather qui utilisait la contra-variance bien plus sure (et qui avait par ailleurs un arbre des classes bien plus intéressant).

        Sinon, c'est clair que l'INRIA n'est pas trop sur les langages de script. Je ne parlais que de Perl6 (et non de Perl5 qui a son propre historique) dont les règles du langage sont elles même définies en regex et qui intègre en son cœur la notion de grammar… Bref, le langage tape dans beaucoup de paradigme en essayant de garder les concepts assez dissociés les uns des autres (aussi un peu comme Sather et non comme Eiffel qui cherchait à tout unifier) avec aussi du boulot (de fou) au niveau de la VM ! Bref, pour un chercheur en science du langage informatique, il y avait de quoi vraiment s'éclater vu que tout était ouvert et il y a, je pense, encore de quoi faire ;-)

      • [^] # Re: Perl6

        Posté par  . Évalué à 5.

        Ça n'a pas vraiment de sens sur ce contexte de dire "l'INRIA pousse ci plutôt que ça"; personne ne nous a demandé de travailler sur tel ou tel langage, c'est chaque chercheur qui choisit le domaine qui lui paraît le plus intéressant ou motivant pour ses recherches. Il y a un peu de pilotage de la recherche dans un institut (par le choix des recrutements) et au niveau national (par le choix des financements), mais c'est à un niveau bien plus grossier ("plus de machine learning et de bio-informatique à tel endroit", "renforcer la cryptographie ici") que le choix d'un langage parmi d'autres.

        Une des premières visites que j'ai faites cette année c'est à l'équipe RMOD à Lille, qui travaille sur le langage Pharo, un des héritiers de Smalltalk et Squeak les plus actifs. De l'autre côté, à Sophia-Antipolis, Manuel Serrano travaille sur Hop, un langage multi-tiers sur le web, maintenant un dialecte de Javascript mais utilisant son implémentation de Scheme. Une partie de l'équipe Celtique à Rennes travaille sur la formalisation de programmes Javascript. Il y a de la recherche en langages dynamiques à l'INRIA.

    • [^] # Re: Perl6

      Posté par  . Évalué à 5.

      Ce qui donne envie aux gens d'étudier la théorie d'un langage, ce n'est pas le fait qu'il ait beaucoup de fonctionnalités différentes. Ça c'est plutôt repoussant, au contraire. C'est le fait qu'on puisse regarder des fonctionnalités originales, qui n'existent pas dans d'autres langages et n'ont pas été étudiées, et apportent soit une grande expressivité soit donne des propriétés intéressantes au langage. Pour Perl6, si quelqu'un voulait l'étudier, je ne sais pas trop ce qu'il faudrait regarder. Quelles sont ses fonctionnalités uniques ?

      Les grammaires Perl6 sont intéressantes, mais on a déjà des langages de grammaires extensibles, et il n'est pas forcément clair de trouver des problèmes difficiles à résoudre dans ce domaine. Les hyper-opérateurs sont rigolos, mais ces idées existent déjà dans les langages à tableaux qui sont étudiés (et plus simples que Perl6 donc plus attirants pour se concentrer sur cette fonctionnalité), voir le travail sur Remora par exemple. Enfin, il y aurait peut-être les jonctions, qui sont amusantes aussi, mais je dirais que c'est plus du travail de linguistique (donner une explication du comportement attendu des expressions exprimées avec des jonctions en terme d'opérations plus simples). Je pense que si je voulais travailler sur Perl6 je choisirais les jonctions : comment leur donner un sens de manière la plus générale possible, en évitant les exceptions et cas particuliers ?

      • [^] # Re: Perl6

        Posté par  (site web personnel) . Évalué à 4.

        Question vérification, dans le domaine du hardware (vhdl), il existe des tas d'outils "d'equivalence checking".

        En gros, ses outils vérifient formellement que 2 descriptions hardware sont équivalentes, bien que complètement différentes (VHDL haut niveau vs description de porte).

        Est-ce qu'il existe des langages ou des outils qui font cela sur des langages répandus ?

        "La première sécurité est la liberté"

        • [^] # Re: Perl6

          Posté par  . Évalué à 7.

          Non, et il y a au moins deux raisons :

          • C'est plus difficile. Dans le domaine du hardware les domaines d'entrée sont finis (des bus de N bits) et se prêtent très bien à la vérification automatique (grosses formules SAT, etc.). Dans le domaine du software les domaines d'entrées sont plus compliqués ("une URL", "un fichier JPEG"), et les logiques plus compliquées.

          • La communauté du hardware est très en avance culturellement à cause du coût des erreurs. La communauté software, et en particulier la communauté du logiciel libre, est en retard sur l'adoption d'outils de vérification.

          On commence à avoir des outils pour prouver que deux programmes sont équivalents, mais en général de façon non-automatique. C'est utilisée par exemple comme une façon de faire des preuves de correction : tu écris un programme efficace/optimisé que tu veux utiliser en production, et un programme simple et naïf que tu utilises comme "spécification" (ou implémentation de référence), et tu essaies de montrer qu'ils sont équivalents.

          P.S.: Il y a un exception notable, qui est le test d'équivalence entre deux automates. Il y a des outils pour faire ça qui sont utilisés dans certaines communautés (en fait on teste plus souvent le vide, le fait qu'un automate accepte au moins une entrée, mais les deux problèmes sont proches). On peut voir les automates (à état finis, à pile, à poil ras, etc.) comme des cas particuliers de programmes très contraints avec de bonne propriétés—une partie des outils de Model Checking utilise ces idées, par exemple.

          • [^] # Re: Perl6

            Posté par  (site web personnel) . Évalué à 3.

            "tu écris un programme efficace/optimisé que tu veux utiliser en production, et un programme simple et naïf que tu utilises comme "spécification" (ou implémentation de référence), et tu essaies de montrer qu'ils sont équivalents."

            ou l'inverse, la version simple étant le modèle de teste. As-tu des noms de langages qui font ça ?

            "La première sécurité est la liberté"

            • [^] # Re: Perl6

              Posté par  . Évalué à 2.

              Dans un assistant de preuve qui permet aussi de programmer, le fait de pouvoir faire ça est une propriété "émergente" du système, c'est un style de preuve parmi d'autres (preuves par raffinement, par logique de programme, etc.). Par exemple, cette technique est utilisée dans le framework / la bibliothèque Bedrock, conçue pour écrire des programmes bas-niveau vérifiés dans l'assistant de preuve Coq.

              • [^] # Re: Perl6

                Posté par  (site web personnel) . Évalué à 5.

                "Our code releases tend to be quite specific to exact Coq versions, so don't expect any of the below to work in any Coq version beside the one specified; yes, even newer versions that are only off by a few characters!"

                Sérieux ! Les scientifiques devraient un peu plus se pencher sur l’intérêt de la compatibilité ascendante ! C'est impossible d'utiliser ce genre de code avec ce genre de contrainte. C'est la deuxième fois que je vois ce genre de problème avec un code issue du publique.

                "La première sécurité est la liberté"

                • [^] # Re: Perl6

                  Posté par  (site web personnel) . Évalué à 8. Dernière modification le 09 février 2018 à 08:50.

                  Une autre question, est-ce que vous faites des rencontres avec des codeurs pour qu'ils exposent leur problème de la "vie réelle". Je suis souvent soufflé par le manque de contexte des chercheurs en informatique que je rencontre.

                  Un dev génial d'un nouveau langage qui est surpris d'apprendre qu'il existe des programmes qui se chiffrent en millions de ligne de code. Un chercheur en compilation qui ne comprends que très vaguement les contraintes hardwares des cpu modernes (false sharing sur les lignes de cache, dépendances read-after-write, write buffer,…). Un codeur linux qui cherche une solution précise dans la littérature scientifique sur un problème de lock, mais il ne trouve que des solutions mono-cpu, ce qui n'existent plus.

                  Pourquoi rien n'est venu remplacer IEEE754 qui est une horreur à traiter automatiquement, car il n'y a aucune propriétés mathématiques utilisables ?

                  Bref, cela aurait un sens d'organiser les "rencontres recherche et développeurs", avec les développeurs qui exposent leur problèmes, et les scientifiques qui expliquent leur solution. Qu'en penses-tu ?

                  "La première sécurité est la liberté"

                  • [^] # Re: Perl6

                    Posté par  (site web personnel) . Évalué à 3.

                    En plus de IEEE754 que je trouve utile pour les cpu, mais compliquer pour les développeurs et les compilateurs, il y a bien d'autre sujet difficile à creuser.

                    Je pense à l'usage par des langages des instructions cpu un peu spécifique, il y a eu le SIMD qui a entrainé l’auto-vectorisation dans GCC, mais il y a plein d'autre instruction ésotérique comme pour aes ou la manipulation de bit (popcount).

                    Il y a le refactoring de code, on peut par exemple penser à la sortie d'une nouvelle version de lib, et le bordel, l'énergie dépensée uniquement pour porter les applications dans la nouvelle version. Je crois que le problème s'est posé avec Qt4 et Gtk3. On pourrait imaginer un moyen de décrire sémantiquement la migration automatiquement un programme d'une version de lib à l'autre.

                    Concernant le test, avec mon expérience dans le code aéronautique, il manque des outils pour générer automatiquement des entrées, pour "couvrir" totalement le code. Ensuite, il faut un moyen pour valider les sorties. Le plus simple est un modèle complet de test. Si on a un "équivalence checker" pas besoin du générateur d'entrée. Les techniques de "fuzzer" s'approche de ce modèle, mais sans garanti sur la couverture du code. Par définition plus un code est complexe, et moins il est couteux de redévelopper un code différent de test, que de faire une couverture total par des tests classiques.

                    Pour aller encore plus loin, même si il existe des outils proprio qu'il le fait, on pourrait imaginer des tag pour faire la traçabilité entre la spec, le code, procédure de test et code de tests. Ainsi on peut savoir ce que les tests valident. On peut vérifier que les tests du 1.1 de la spec, couvre bien entièrement le code lié au point 1.1, et non pas un autre test qui le fait par hasard et sans vérifier les sorties (vécu). Si un outil vérifie la cohérence de l'ensemble, il devient facile d'estimer l'impact dans un projet en cas de modification de spec. Actuellement, c'est fait avec divers outils, Excel inclus.

                    J'imagine qu'il y a plein d'autres problèmes de ce genre.

                    "La première sécurité est la liberté"

                • [^] # Re: Perl6

                  Posté par  (site web personnel) . Évalué à 3.

                  Le cas de Coq est un peu particulier, parce qu'il s'agit en fait d'au moins deux langages différents, Gallina, le langage de preuve en tant que tel, et Ltac, un langage de métaprogrammation qui est à Gallina ce que PHP est à HTML. Autant Gallina est plutôt bien spécifié[1], autant Ltac est un bousin sans nom qui est la source d'un tas de problèmes, le genre de code qu'il suffit de regarder fixement pour faire péter un développement à l'autre bout de la planète. Ceci dit, il y a eu du progrès depuis et l'utilisation d'une infrastructure d'intégration continue un peu sérieuse permet de jauger la casse avant la publication d'une version.

                  En ce qui concerne Bedrock, je me permets quand même de juger que c'est un cas vraiment extrême. C'est un projet notablement connu pour avoir été implémenté par des gens qui sont des spécialistes internationaux de l'exploitation de bug à des fins particulièrement créatives. Personnellement, ma réaction naturelle serait de les secouer très fort jusqu'à ce qu'ils comprennent que ce qu'ils font donne des envies suicidaires et/ou meutrières à l'équipe de développement de Coq.

                  [1] Bon en fait, n'importe quel spécialiste de la théorie des types sait que c'est pas vrai non plus, mais au moins c'est un langage plutôt robuste en terme de compatibilité.

                  • [^] # Re: Perl6

                    Posté par  . Évalué à 2. Dernière modification le 09 février 2018 à 21:26.

                    Ltac est un bousin sans nom qui est la source d'un tas de problèmes, le genre de code qu'il suffit de regarder fixement pour faire péter un développement à l'autre bout de la planète.

                    Justement, au sujet de Ltac, vous avez des idées ou des pistes pour l'améliorer et faciliter l'écriture de tactiques ? Si on prend l'exemple de patrick_g :

                    Par exemple dans de nombreux articles de géométrie arithmétique ou de géométrie algébrique on peut voir des phrases du style : "Par un argument à la GAGA il est facile de voir que blabla".

                    il doit bien être possible d'écrire une tactique gaga, mais ce possible reste souvent « théorique », écrire une tactique finissant par rendre à moitié fou (j'ai jamais bien compris comment marchait le système).

                    Sapere aude ! Aie le courage de te servir de ton propre entendement. Voilà la devise des Lumières.

        • [^] # Re: Perl6

          Posté par  (site web personnel) . Évalué à 2.

          D'une manière générale, l'équivalence de programme est indécidable, donc ça limite énormément les choses.
          Cependant, de mémoire, il existe des languages de niches avec des propriétés de sorte que certaines équivalences soient décidables. Je dis bien "certaines équivalences", car les définitions d'équivalence ne manquent pas.
          Dans d'autres cas, tu dois toi-même fournir ta preuve, et utiliser un assistant pour la vérifier. Aucun souvenir du nom de telles applications, mais je me souviens vaguement d'un outil calculant des bisimulations pour le langage LOTOS.

          Enfin, ça fait des années que je n'ai plus mis les pieds dans ce domaine, et quand j'y étais encore mon labo était plus théorique qu'appliqué en terme d'équivalence…

  • # Math

    Posté par  (site web personnel) . Évalué à 8. Dernière modification le 17 mai 2018 à 09:13.

    Aujourd’hui quand quelqu’un annonce un nouveau résultat mathématique, il peut être très difficile de savoir si le résultat est correct ou non ; il sera peut-être un jour réaliste de demander à la personne de fournir une preuve vérifiée par un assistant de preuve, pour accélérer son étude et sa compréhension par les scientifiques du domaine.

    Je ne comprends pas du tout cette phrase.
    Actuellement quand un résultat de math est démontré par un chercheur (la preuve du dernier théorème de Fermat par Wiles par exemple) alors le chercheur écrit un article à destination de ses collègues pour expliquer sa démonstration.
    Les collègues lisent l'article, évaluent la rigueur et la pertinence des arguments et finalement portent un jugement sur la véracité de la démonstration.
    Ce qu'il faut bien voir c'est que l'auteur écrit son article pour optimiser la compréhension auprès de ses collègues. Ce sont eux (les pairs) qui vont évaluer son travail.
    L'article n'est pas écrit dans un langage formel évaluable par une machine. Il est écrit avec des phrases et des mots.
    Certains points, considérés comme de la routine pour les spécialistes du domaine, sont abrégés ou carrément passés sous silence.
    Par exemple dans de nombreux articles de géométrie arithmétique ou de géométrie algébrique on peut voir des phrases du style : "Par un argument à la GAGA il est facile de voir que blabla".
    Les spécialistes comprennent immédiatement que cela fait référence à l'article ultra-connu de Jean-Pierre Serre intitulé "Géométrie algébrique et géométrie analytique".
    Mais une machine ne comprendrait pas ça. Pour une machine tout doit être complètement formalisé.

    Donc tout ça pour dire que ta phrase affirmant qu'une démonstration "vérifiée par un assistant de preuve accélérait son étude et sa compréhension par les scientifiques du domaine" ne tient pas debout. Cette preuve serait au contraire illisible par un humain si on la compare aux articles actuels qui, eux, sont écrits pour des humains.
    La vérification formelle des démonstrations pourra sans doute être très utile pour avoir la certitude qu'il n'y a pas d'erreurs qui se sont glissés dans le raisonnement. C'était le pari de Voevodsky.
    Mais il y a très peu de chance pour que, en soi, cela favorise la compréhension.

    • [^] # Re: Math

      Posté par  (site web personnel) . Évalué à 6.

      Le problème que tu oublies est que le nombre de personnes ayant les compétences pour vérifier réellement la démonstration du théorème de Fermat est d'une dizaine de personne dans le monde. Une preuve formelle permet justement de ne pas avoir besoin de ça.

      Ensuite, si tu veux faire référence à un résultat qui existe déjà, c'est facile d'imaginer des libraries pour ça. Quand tu rentres dans les détails, c'est toujours plus simple de lire du code, que de décoder ce que voulait dire l'auteur d'un texte.

      "La première sécurité est la liberté"

      • [^] # Re: Math

        Posté par  (site web personnel) . Évalué à 4.

        Une preuve formelle permet justement de ne pas avoir besoin de ça.

        Une preuve formelle te donne juste un résultat binaire. Oui la démonstration est juste ou bien Non y'a une merde.
        Elle ne t'explique pas l'idée clé. Elle ne te fait pas comprendre intuitivement pourquoi la démonstration fonctionne.

        Ensuite, si tu veux faire référence à un résultat qui existe déjà, c'est facile d'imaginer des libraries pour ça

        Bien entendu. C'est pourquoi j'avais fait référence au boulot de Voevodsky (voir ici). Mais encore une fois cela ne communique pas l'idée de la démonstration.

        • [^] # Re: Math

          Posté par  . Évalué à 3.

          Elle ne t'explique pas l'idée clé.

          Il y a plusieurs niveaux d'analyse, mais je dirais quand même qu'en maths, un théorème est démontré si sa démonstration est prouvée, et c'est tout. Si tu as une preuve formelle mais que la démonstration est tellement tortueuse que personne ne la comprend, ça ne retire rien de la réalité de cette démonstration; tu pourras réutiliser le résultat du théorème pour d'autres démonstrations, et voila.

          • [^] # Re: Math

            Posté par  . Évalué à 2.

            Je ne suis pas d'accord : si seule l'existence d'une preuve primait, personne ne chercherait à re-prouver un résultat déjà établi.

            Or les nouvelles preuves de résultats déjà connues sont très courantes et très importantes : on cherche aussi de nouveaux biais d'attaque des problèmes, de nouveaux éclairages, plus d'élégance…

            • [^] # Re: Math

              Posté par  (site web personnel) . Évalué à 2.

              Je ne suis pas d'accord : si seule l'existence d'une preuve primait, personne ne chercherait à re-prouver un résultat déjà établi.

              Je ne vois pas trop en quoi tu exprimes un désaccord avec arnaudus.

        • [^] # Re: Math

          Posté par  (site web personnel) . Évalué à 4.

          Oui, mais ce n'est pas avec "l'idée" que tu as assez d'information pour savoir si c'est bidon ou nécessaire et suffisant.

          "La première sécurité est la liberté"

        • [^] # Re: Math

          Posté par  . Évalué à 6.

          Une preuve formelle te donne juste un résultat binaire. Oui la démonstration est juste ou bien Non y'a une merde.
          Elle ne t'explique pas l'idée clé. Elle ne te fait pas comprendre intuitivement pourquoi la démonstration fonctionne.

          Attention, je ne suis pas d'accord. Une preuve formelle est un document qui décrit la preuve en assez de détails pour être vérifiée par un ordinateur. En particulier, elle contient assez de détails pour être relue et comprise par un humain. Elle n'est pas plus "binaire" en cela qu'une preuve en LaTeX.

          La question est de savoir si la personne a fait assez d'efforts, en organisant sa preuve mécanisée, pour que l'argument de preuve soit clair et que la preuve puisse être comprise. (Un programme informatique aussi peut être "correct", faire ce qu'on attend, mais illisible par un autre humain. Une preuve LaTeX aussi peut être incompréhensible.)

          Aujourd'hui les outils que nous utilisons pour écrire les preuves mécanisées gênent un peu pour écrire des preuves vraiment agréables à relire—d'où l'habitude de maintenir aussi une preuve informelle en LaTeX en parallèle. On travaille à améliorer cela aussi, et aujourd'hui il est déjà possible en faisant des efforts (de la part de l'auteur, surtout, mais aussi du lecteur) de présenter des preuves mécanisées qui sont aussi lisibles/compréhensibles.

          (Je pense que tu as en tête une image des preuves vérifiées basées seulement sur la démonstration automatique, où on demande à l'ordinateur de reconstruire l'argument de preuve sans aucune information (le SAT/SMT-solving par exemple). Quand on utilise un assistant de preuve, on peut (et on doit) donner les arguments de preuve à l'assistant, dès qu'on veut démontrer des propriétés plus complexes/intéressantes que ce qui est facile à vérifier par une machine.)

    • [^] # Re: Math

      Posté par  . Évalué à 4.

      Sauf qu’aujourd’hui certaines preuves utilisent des ordis pour faire des bouts de démonstration. Ça complique les choses d’une part parce que si tu veux enlever l’algo de l’équation ça produit des preuves dont la taille est sans commune mesure avec les preuves d’avant. Donc un truc probablement fastidieux et long à vérifier à la main, on a ptete mieux à faire du temps et des nerfs de nos meilleurs matheux. Ou alors ça nécessite de se convaincre que le programme utilisé est effectivement capable de produire une démonstration de ce qu’il est supposé montrer. Donc qu’il est sans bug. Les matheux tradis détestent ces démonstrations d’ailleurs, parce que les ordis servent souvent à faire une exploration systématique d’un certain nombre de cas qui peuvent exploser combinatoirement, et qu’ils préfèreraient un argument qui règle tout de manière plus synthétique avec une belle théorie. Et que ça rend difficile de se convaincre de la correction de la preuve. Mais rien ne dit que ça existe dans l’absolu et que toutes les preuves sont « courtes ». Au contraire est certains qu’il y a des objets comme des indécidables ou des propositions à démonstrations très très longue dans un système logique donné. cf. https://fr.wikipedia.org/wiki/Longueur_d%27une_d%C3%A9monstration

      Par exemple pour P=?NP ou des « preuves » sont produites régulièrement par tout un chacun et envoyés à des experts, il y a de bonne chances pour que personne ne lise jamais la proposition, trop long et peu probable que ce soit correct de la part d’un non expert du domaine. Si ça se trouve elle a été trouvée mais personne n’a ouvert le mail et elle a zéro chances d’être publiée :) Si le type fournit une preuve prouvée (inception) il a peut être plus de chances d’être pris au sérieux.

    • [^] # Re: Math

      Posté par  . Évalué à 5.

      L'idée n'est pas de remplacer le document décrivant la preuve par le code de la preuve mécanisée, mais de le complémenter. Aujourd'hui la preuve LaTeX a deux rôles, à la fois communiquer le résultat et s'assurer, du mieux possible, qu'il n'y a pas d'erreurs. C'est agréable quand on est un lecteur qui sait que la preuve a déjà été acceptée par la communauté et qui peut se concentrer sur la compréhension, mais pas pour :

      • les premiers rapporteurs/relecteurs, qui ont une lourde responsabilité vis-à-vis de la communauté et à qui la partie "re-vérifier les calculs et les arguments" peut demander énormément de travail (en plus du travail de compréhension d'ensemble, etc.)
      • l'auteur lui-même, qui n'a pas d'outils adapté pour, par exemple, savoir quelles parties du développement doivent être revues si il ou elle modifie une définition ou change une hypothèse

      (Un exemple un peu extrême est la démonstration proposée de la conjecture ABC, qui a été proposée à la communauté en 2012 et dont on ne sait toujours pas si elle acceptée ou pas.)

      Quand on utilise un assistant de preuve, les rapporteurs/reviewers doivent d'une part comprendre l'argument d'ensemble (comme avant) et les idées des preuves (comme avant). Pour savoir si les preuves sont correctes dans les détails, il suffit de lire les énoncés de la preuve mécanisée, et de se convaincre qu'ils correspondent effectivement aux énoncés de l'article informel (il peut bien sûr y avoir des erreurs à ce niveau-là); re-vérifier indépendamment la preuve mécanisée est ensuite "immédiat" (on fait tourner le programme vérificateur de preuve), et donne une confiance très forte dans la validité de la démonstration. Ça aide aussi beaucoup l'auteur en cas de modification de la preuve au cours de son écriture.

      Une partie de ma communauté travaille déjà comme ça : dans certaines de nos conférences il y a un tiers (je dirais, à la louche) des soumissions qui viennent avec, en complément, une preuve mécanisée, et cela nous a permis d'attaquer des problèmes plus difficiles et de faire des raisonnements plus techniques avec confiance, et en gardant des temps de revue/relecture relativement courts (quelques mois).

      (C'est aussi absolument nécessaire pour la preuve de programmes, où on écrit une preuve mathématique du fait qu'un programme correspond à une spécification. La nature très calculatoire de certaines parties de ces arguments fait qu'il est extrêmement pénible de relire les détails des preuves pour un humain, et que le risque d'erreur d'inattention augmente beaucoup.)

      Un exemple typique est le livre "Homotopy Type Theory", qui a été entièrement formalisé avec un assistant de preuve (en Agda), en parallèle avec la rédaction du livre dans un style "informel" (non vérifié) mathématique classique.

    • [^] # Re: Math

      Posté par  (site web personnel) . Évalué à 4.

      le chercheur écrit un article à destination de ses collègues pour expliquer sa démonstration.

      Ou plutôt "le chercheur écrit un article à destination d'une conférence où le nombre de pages de chaque publication est limité et la taille de la police est imposée." Même certains journaux ont des limites de pages…

      • [^] # Re: Math

        Posté par  (site web personnel) . Évalué à 3. Dernière modification le 09 février 2018 à 22:39.

        le chercheur écrit un article à destination d'une conférence où le nombre de pages de chaque publication est limité

        Alors ça, il me semble que ces articles à destination des conférences et avec pagination imposée ça se fait plutôt dans le domaine de la recherche en informatique non ?
        Ce n'est plus vrai du tout en math pures ou on voit passer des très gros articles et les journaux n'ont pas peur de publier ça (et ne semblent pas limités par la pagination).
        Si je regarde sur la page de Peter Scholze (qui a 99,999% de chances de recevoir la médaille Fields cet été) je trouve ça pour les papiers postées ces deux dernières années :

        Topological Hochschild homology, and integral p-adic Hodge theory => 84 pages
        Étale cohomology of diamonds => 154 pages
        Integral p-adic Hodge theory => 118 pages
        On the generic part of the cohomology of compact unitary Shimura varieties => 98 pages

        Et je ne parle même pas du multiplodocus de Fargues-Fontaine (soumis à Astérisque qui publie des monographies):

        Courbes et fibrés vectoriels en théorie de Hodge p-adique => 399 pages

        • [^] # Re: Math

          Posté par  (site web personnel) . Évalué à 2.

          Tu es sur que ce sont toutes des "publications" ? Ton dernier exemple ressemble plus à un bouquin qu'à une publication. Avec l'édition électronique, la frontière entre les deux va se réduire mais en gros, un publication est ciblé sur un problème particulier et est intégré dans un ensemble : conférence, revue… Je suis surpris qu'on puisse nommé "publication" un document qui a une préface écrite par une autre personne.

          Bref, je crois qu'ici, on parlait de publication dans le sens publication dans une revue ou dans une conférence.

          • [^] # Re: Math

            Posté par  (site web personnel) . Évalué à 3.

            Oui le dernier exemple est tellement gros qu'il va être publié comme une monographie.
            Mais je maintiens ce que j'ai dit : en math pures il se publie de très gros articles dans les journaux.
            L'exemple 4 des papiers de Scholze a été publié dans Annals of Math (lien).
            Regarde aussi celui-ci qui fait 121 pages, également publié dans Annals of Math.
            Et pas que Annals, d'autres journaux aussi. Les Publications Mathématiques de l'IHES par exemple sont connues pour accepter de très gros papiers (l'héritage des EGA/SGA de Grothendieck ?). En allant jeter un coup d'oeil rapide je tombe sur cet article qui fait plus de 150 pages.

            • [^] # Re: Math

              Posté par  . Évalué à 4.

              Bon, c'est bien joli de compter les pages de tes articles préférés (ma communauté aussi a des articles longs pour les journaux, même si ça n'est pas toujours très apprécié par les relecteurs), mais tu avais commencé ce fil "Math" avec une discussion un peu plus profonde sur les preuves dans l'activité mathématique (à comparer peut-être avec l'article de 1979 Social Processes and Proofs of Theorems and Programs, très critique de l'idée de preuve mécanisée), et je serais curieux de savoir si cette discussion a dissipé nos différences de point de vue, ou si tu continues à ne pas être convaincu par l'idée que les assistants de preuve pourraient un jour apporter du confort à la pratique de la recherche en mathématiques.

              • [^] # Re: Math

                Posté par  . Évalué à 1.

                Je pense que c'est déjà le cas pour certains mathématiciens. Dans Théorème vivant on voit que Cédric Villani et Clément Mouhot utilisent un outil de calcul formel pour manipuler leurs équations ainsi que Coq pour vérifier leurs démonstrations.

                • [^] # Re: Math

                  Posté par  . Évalué à 2.

                  Je suis très surpris d'apprendre que Coq aurait été vérifié par Villani (je pense que ce n'est pas possible vu son domaine de travail et l'état de la formalisation mécanisée en analyse et en probabilités), je pense que tu as mal compris—mais je n'ai pas accès au livre pour vérifier. Le calcul formel est évidemment utilisé, mais il ne s'agit pas de la même chose (il s'agit d'une aide au calcul, pas d'une vérification des preuves elles-mêmes).

                  • [^] # Re: Math

                    Posté par  . Évalué à 2.

                    J'ai écrit que Villani et Mouhot avaient utilisé Coq pour vérifier leurs démonstrations : celles de Villani et Mouhot. Ils ne travaillent pas sur Coq mais avec Coq.

                    • [^] # Re: Math

                      Posté par  . Évalué à 2.

                      C'est bien ce que j'ai compris (j'ai écrit "vérifié" ci-dessus mais je voulais dire "utilisé", merci LinuxFR de ne pas permettre d'éditer les messages après-coup), et je pense que ce n'est pas vrai.

                      • [^] # Re: Math

                        Posté par  . Évalué à 1.

                        Oui tu as raison, j'ai retrouvé où C. Villani en parle dans son bouquin : chapitre 31, où il parle de sa rencontre avec Voevodsky dans un parc à Princeton, de la preuve du théorème des quatre couleurs, de l'Inria, de Georges Gonthier et son travail sur COQ.

              • [^] # Re: Math

                Posté par  (site web personnel) . Évalué à 4.

                je serais curieux de savoir si cette discussion a dissipé nos différences de point de vue, ou si tu continues à ne pas être convaincu par l'idée que les assistants de preuve pourraient un jour apporter du confort à la pratique de la recherche en mathématiques.

                Honnêtement je ne sais pas. Voevodsky pensait que la complexité de la recherche en géométrie algébrique était devenue telle qu'il fallait absolument changer le paradigme et utiliser ces assistants de preuve pour être certains de ne pas faire d'erreur dans les démonstrations. D'après ce que j'ai lu ses collègues ne semblent pas convaincus et ils continuent de faire leur recherche et de publier leurs démonstrations de façon classique.

                Peut-être qu'il faudra attendre que ces assistants deviennent plus puissants, plus simples à utiliser et qu'ils s'appuient sur des bibliothèques bien plus complètes de résultats déjà démontrés.
                Ou peut-être qu'il y aura une séparation du travail et qu'on va assister à l'émergence d'une nouvelle classe de mathématiciens. Ces nouveaux chercheurs prendront les résultats démontrés classiquement et feront le travail de vérification formelle. Un peu ce qu'à fait Gonthier avec la vérification du théorème de Feit-Thompson.
                Mais ça lui a pris 6 ans, il était entouré d'une équipe de chercheurs et c'était pour prouver un théorème vieux de plus de 50 ans.
                Autrement dit c'est pas gagné…

  • # Ocaml et Float

    Posté par  (site web personnel) . Évalué à 2.

    Tiens tant que j'y suis, puisque tu passes du temps sur Ocaml. Pourquoi vous n'avez jamais trouvé un moyen d'éviter d'utiliser les insupportables opérateurs float (+.),(-.),(/.),(*.) ?

    Ça rend l'utilisation des float en Ocaml quasi inutilisables…

    « Il n’y a pas de choix démocratiques contre les Traités européens » - Jean-Claude Junker

    • [^] # Re: Ocaml et Float

      Posté par  . Évalué à 3.

      Pourquoi vous n'avez jamais trouvé un moyen d'éviter d'utiliser les insupportables opérateurs float (+.),(-.),(/.),(*.) ?

      Il y a une proposition pour résoudre ce problème, et offrir bien plus de possibilité, sous la forme de modules implicites. Il y a eu une discussion sur le sujet sur le forum OCaml, et il reste des questions tant théoriques que pratiques (au niveau de l'implémentation) à résoudre avant de voir apparaître le système dans le langage.

      Pour faire simple, l'idée est de passer par des modules de premières classes et, dans le cas de ces opérateurs, de définir, disons, un type de module pour les corps :

      module type CORPS = sig
  type t
  val zero : t
  val one : t
  val add : t -> t -> t
  val sub : t -> t -> t
  val mul : t -> t -> t
  val div : t -> t -> t
end

      puis à définir, disons une fonction add, qui opère sur n'importe quel corps et des valeurs du support du corps :

      let add (type a) (module M : CORPS with type t = a) x y = M.add x y;;
val add : (module CORPS with type t = 'a) -> 'a -> 'a -> 'a = <fun>

      Ici le corps à passer en paramètre est explicite et si on utilise l'alternative Batteries à la bibliothèque standard, on peut écrire :

      add (module Float) 2.3 4.5;;
- : float = 6.8

      L'idée étant de faire du module de première classe un paramètre implicite déterminé automatiquement par le compilateur en fonction du type des paramètres x et y. Ici comme ce sont des float, le compilateur cherchera dans son environnement au moment de l'appel à add un corps sur les float déclaré utilisable comme arguments implicites.

      En attendant, si tu utilises Batteries tu peux écrire ton code sur les flottants via des open locaux :

      let open Float.Infix in 2.3 + 4.5;;
- : float = 6.8

      voir la définition du module Float.Infix :

      #show_module Float.Infix;;
module Infix = BatFloat.Infix
module Infix :
  sig
    type bat__infix_t = float
    val ( + ) : float -> float -> float
    val ( - ) : float -> float -> float
    val ( * ) : float -> float -> float
    val ( / ) : float -> float -> float
    val ( ** ) : float -> float -> float
    val ( -- ) : float -> float -> float BatEnum.t
    val ( --- ) : float -> float -> float BatEnum.t
    val ( =~ ) : ?epsilon:float -> float -> float -> bool
  end

      Sapere aude ! Aie le courage de te servir de ton propre entendement. Voilà la devise des Lumières.

  • # Que penses-tu de mon langage préféré : le Rust ?

    Posté par  (site web personnel) . Évalué à 1.

    Une des choses que j'aime, c'est le multi-paradigme ; mais évidemment ce qui m'a séduit c'est la nouveauté qu'il a introduite : la sécurité mémoire sans GC.

    Du coup, je me dis que (peut-être) ça a un rapport avec ton domaine de recherche, à savoir un langage auto-validé. Par exemple, je sais qu'avec la programmation logique on peut vérifier la validité d'un compilateur, ou encore faire des analyses statiques de code. Je me demande en quoi le Rust permet de répondre à certains de ces problèmes.

Suivre le flux des commentaires

Note : les commentaires appartiennent à celles et ceux qui les ont postés. Nous n’en sommes pas responsables.