Journal Déterminer un code à 3 chiffres en 9 questions ou moins

Posté par  . Licence CC By‑SA.
Étiquettes : aucune
17
23
mar.
2019

Bonjour nal,

Aujourd'hui, j'ai fait un escape grotte à proximité de Montpellier. C'est comme un escape game mais dans une grotte naturelle. C'était fort joli, mais ce n'est pas pour ça que je viens te voir.

Dans cette grotte, une des énigmes était la suivante : nous étions face à un individu muet, à qui nous pouvions poser des questions auxquelles il ne pouvait répondre que par oui ou non. Nous devions obtenir le code à 3 chiffres de 0 à 9 d'un coffre et nous ne disposions que d'un essai pour composer le code. Nous pouvions poser autant de questions que nous voulions mais nous avions un bonus si nous trouvions en 9 questions ou moins.

Nous avons trouvé en 10 questions par dichotomie. Nous avons d'abord demandé si le nombre était supérieur ou égal à 512 (non) puis à 256 (non), puis à 128 (oui), puis à 192, et ainsi de suite jusqu'à obtenir le nombre exact. Cette méthode trouve à coup sûr un nombre entre 0 et 1023 en 10 questions.

Je me demandais, journal, si tu avais une idée pour trouver le code à coup sûr en 9 questions ou moins, ou une démonstration que c'est impossible.

  • # Modulo

    Posté par  (Mastodon) . Évalué à -4.

    J'ai du mal à réfléchir mais la procédure suivante n'est-elle pas plus rapide ?
    1. Le nombre X recherché peut s'écrire X = Q*7 + R.
    2. Poser la question: Quel est le reste de la division par 7? On connaît R
    3. Q est largement inférieur à 143. J'imagine qu'il faut moins de 8 questions par dichotomie pour le trouver, non ?

    Clairement, il y a moyen d'optimiser la procédure pour être plus efficace encore.

    Surtout, ne pas tout prendre au sérieux !

    • [^] # Re: Modulo

      Posté par  . Évalué à 8.

      1 question le reste de la division par 10001 :)
      la reponse est oui ou non pas un chiffre

  • # avec des divisions

    Posté par  (site web personnel) . Évalué à 6.

    On peut en effet poser des questions autrement en jouant sur les diviseurs, on réduit très vite les possibilités. Par exemple sur deux chiffres :

    le code est il divisible par trois ?

    1. Oui ? on a plus que 3 possibilités par dizaines, plus 00, 30, 60 et 90, ça fait 34 réponses ;
    2. Non ? ça fait 76 réponses.

     le code est il divisible par cinq ?

    1. Si oui par 3 et oui par 5 on a 7 réponses
    2. Si oui par 3 et non par 5 on a 27 réponses
    3. Si non par 3 et non par 5 on a 68 réponses
    4. Si non par 3 et oui par 5 on a 8 réponses

    le code est-il divisible par deux ?

    • Dans tous les cas, on divise le résultat précédent par deux.

    En trois questions, on a donc réduit à 4, 14 ou 34 possibilités.

    "La liberté est à l'homme ce que les ailes sont à l'oiseau" Jean-Pierre Rosnay

    • [^] # Re: avec des divisions

      Posté par  . Évalué à 7.

      Bien vu de décomposer le code en produit de facteurs premiers.

      Malheureusement, ça me semble moins efficace (dans le pire des cas) que la méthode donnée dans le journal (d'ailleurs pourquoi 512 et pas 500 ?).

      Le pire des cas étant 997. Est-ce que c'est divisible par 2 ? Non. 3 ? Non. 5 ? Non. 7 ? Non. 11 ?…

      Et là, ça fait 168 questions. C'est un peu beaucoup.

      • [^] # Re: avec des divisions

        Posté par  (site web personnel) . Évalué à 2.

        J'ai pris un exemple simple sans beaucoup y réfléchir en pensant au casseur de code qui n'a pas de calculette sous la main. Puisque il est impossible de faire mieux que 10 questions, on peut chercher à augmenter fortement la probabilité de trouver en moins de 9 coups. Avec une astuce plus élaborée. Par exemple, à l'une ou l'autre des étapes « Y a-t-il un nombre pair ou plus dans la combinaison ? », « Y a-t-il un nombre divisible par 3 dans la combinaison ? », etc.

        "La liberté est à l'homme ce que les ailes sont à l'oiseau" Jean-Pierre Rosnay

        • [^] # Re: avec des divisions

          Posté par  (site web personnel) . Évalué à 2. Dernière modification le 24 mars 2019 à 14:52.

          D'autre part on peut aussi poser des questions moins mathématiques :

          • sans faire intervenir la chance, est-il possible de trouver la solution en moins de 9 coups ?
          • ce nombre a-t-il été choisi au hasard ?
          • est-ce un nombre premier ?
          • le nombre change-t-il en fonction des participants ?
          • …

          "La liberté est à l'homme ce que les ailes sont à l'oiseau" Jean-Pierre Rosnay

          • [^] # Re: avec des divisions

            Posté par  (site web personnel) . Évalué à 4.

            D'autres ruses possibles, peut-être inutiles :

            • dessine les chiffres sur le sol : 0 1 2 3 4 5 6 7 8 9 et pose une question sur leur forme
            • y a-t-il un chiffre répété ?
            • trouver une question basée sur le nombre de lettres dans le nom des chiffres ; on a :
              • un avec un nom à 2 lettres : 1
              • un avec un nom à 3 lettres : 6
              • six avec un nom à 4 lettres : 2, 7, 8, 9, 0
              • un avec un nom à 5 lettres : 3
              • un avec un nom à 6 lettres : 4
            • on a encore les noms qui contiennent une ou deux voyelles

            "La liberté est à l'homme ce que les ailes sont à l'oiseau" Jean-Pierre Rosnay

    • [^] # Re: avec des divisions

      Posté par  . Évalué à 5.

      Ça ne me semble pas plus efficace. J'ai mis un moment avant de réaliser que tu prenais l'exemple d'un code à 2 chiffres, donc 100 possibilités. Or par dichotomie, en une question tu peux réduire les possibilités à 50, 2 questions = 25 possibilités, 3 questions = 13 possibilités. La dichotomie permet de t'assurer de diviser les possibilités par 2 à chaque fois, ce qui n'est pas le cas des diviseurs (tu risques donc de te retrouver dans une situation "pire").

      Si le nombre est parfaitement aléatoire, il me semble que la dichotomie reste la meilleure solution.

      En revanche, si le nombre a été choisi par les concepteurs du jeu, on peut supposer qu'ils ont sans doute choisi un nombre "forçant" les 10 tentatives. Il convient donc peut-être de varier les méthodes pour réduire le domaine de différentes manières (par exemple en demandant si le code est divisible par deux). Ça se base plus sur la psychologie des concepteurs du jeu que sur une logique mathématique, mais dans ce genre de situation c'est le genre de choses à prendre (aussi) en compte :)

  • # Solution ?

    Posté par  . Évalué à -5. Dernière modification le 24 mars 2019 à 04:17.

    Quel est le résultat modulo 3 du 1er chiffre:
    - 0 (0, 3, 6, 9)
    - 1 (1, 4, 7)
    - 2 (2, 5, 8)

    Si c'est 0, le chiffre est est-il supérieur 5.
    - Si oui alors est-il 6. Si non c'est forcément 9.
    - Si non alors est-il 3. Si non c'est forcément 0.

    Si c'est 1, le chiffre est-il supérieur à 3.
    - Si oui alors est-il 4. Si non c'est 7.
    - Si non c'est 1.

    De même pour 2.

    On a trouvé le 1er chiffre en 3 essais. Faire de même pour les deux autres.

    • [^] # Re: Solution ?

      Posté par  . Évalué à -1. Dernière modification le 24 mars 2019 à 04:32.

      À supprimer.

    • [^] # Re: Solution ?

      Posté par  . Évalué à 4.

      Évidement la solution ne marche pas puisqu'il faut répondre par oui ou par non …

  • # Début de preuve

    Posté par  (Mastodon) . Évalué à 10.

    Pas certain, mais il me semble qu'en fait il n'y a pas moyen de faire mieux que l'algorithme (par dichotomie) proposé pour garantir une réponse en 10 questions.

    En effet, vu que la réponse est oui ou non; chaque question permet de diviser en 2 parties (pas forcément égales) le reste des candidats possibles (indépendamment des questions précédentes).

    Si on prend une approche telle que proposée qui divise en deux parties égales le reste des candidats, on est sur de trouver la réponse en 10 étapes (pas 9 ni 11). On est donc sur de ne pas obtenir le bonus.

    Si on ne divise pas l'ensemble des candidats en deux parties égales, l'algorithme peut terminer plus rapidement qu'en 9 étapes mais peut être beaucoup plus lent. Exemple extrême: l'énumération:
    - Est-ce 000 ?
    - Est-ce 001 ?
    - …
    Avec de la chance vous pouvez terminer en moins de 9 étapes, avec pas de chance,…

    Autre exemple, si vous posez une question comme
    - Y a-t-il un nombre pair ou plus dans la combinaison ?
    Si la réponse est non, vous n'avez plus que 125 candidats restants (vous avez de la chance)
    Si non, il vous en reste 875 :-(

    Pour conclure, il n'y avait pas moyen d'être sur d'obtenir le bonus mais l'approche que vous aviez choisi vous garantissait de ne pas l'obtenir.

    Surtout, ne pas tout prendre au sérieux !

    • [^] # Re: Début de preuve

      Posté par  (site web personnel) . Évalué à 2.

      il me semble qu'en fait il n'y a pas moyen de faire mieux que l'algorithme (par dichotomie) proposé pour garantir une réponse en 10 questions.

      1 risque sur 10 qu'il y a besoin de 10 questions, la dichotomie garantit la réponse en <= 10 questions :-)

      mais l'approche que vous aviez choisi vous garantissait de ne pas l'obtenir.

      bin non, si le nombre était 500, en une question c'est plié ;-)

      • [^] # Re: Début de preuve

        Posté par  (site web personnel) . Évalué à 4.

        Le mieux aurait sans doute été de compter sur la chance au premier coup en tentant 255, ou 744. Si ça se passait bien, vous aviez le bonus. Sinon, il vous fallait jusqu'à 10 questions de plus.

      • [^] # Re: Début de preuve

        Posté par  . Évalué à 4.

        si le nombre était 500, en une question c'est plié

        Non car la question est du genre « le nombre est-il inférieur à 500 ? ».

    • [^] # Re: Début de preuve

      Posté par  . Évalué à 2. Dernière modification le 24 mars 2019 à 19:27.

      et le nombre de lettre du nombre ?

  • # impossible... a moins de tricher

    Posté par  (site web personnel) . Évalué à 10. Dernière modification le 24 mars 2019 à 09:23.

    9 questions qui se répondent par oui ou par non, ça fait juste 9 bits d'informations, soit seulement possible de déterminer parmi 512 possibilités a coup sûr.

    Donc il fait trouver une ruse pour extraire plus d'informations:

    • "si le reste de la division par 3 est 1, réponds oui, si c'est 2, réponds non, sinon ne réponds pas."

    • side channels: Si le nombre est divisible par deux, est-ce que le nombre divisé par deux est pair, Sinon, additiones ✓(1903+3281) au nombre, divise par deux, est ce que le résultat est pair? Et on extrait de l'information en fonction du temps de réponse.

    • [^] # Re: impossible... a moins de tricher

      Posté par  . Évalué à 3.

      Je cherchais une manière d'extraire plus d'informations effectivement. J'aime bien ta première proposition ! (la non-réponse étant elle-même une réponse)

    • [^] # Re: impossible... a moins de tricher

      Posté par  . Évalué à 3. Dernière modification le 05 avril 2019 à 19:56.

      Division de l'espace des possibilités par 3 plutôt que par 2, en posant chaque question ainsi :

      • répond par oui si le nombre est inférieur ou égal à 333,
      • par non s'il est strictement supérieur à 666,
      • ne répond pas sinon.

      Et ainsi de suite… On trouve la réponse en au moins 6, au plus 7 questions (3^6=729, 3^7=2187).

  • # Obligatory XKCD

    Posté par  . Évalué à 7.

    Salut :)

    nous étions face à un individu muet, […] il ne pouvait répondre que par oui ou non

    Un muet qui peut répondre. Bin voyons, ils se seraient pas un peu foutu de toi dans ton grotte-game ? :p

    Solution en une question/réponse :
    drugs+hits

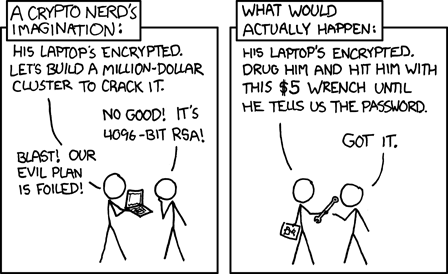
    Voilà, de rien !

    Matricule 23415

    • [^] # Re: Obligatory XKCD

      Posté par  (site web personnel) . Évalué à 2. Dernière modification le 24 mars 2019 à 19:17.

      Un muet qui peut répondre. Bin voyons, ils se seraient pas un peu foutu de toi dans ton grotte-game ? :p

      Voilà pourquoi tu te fait inutiler, il n'est pas sourd, il peut hocher/tourner la tête !

      « Il vaut mieux mobiliser son intelligence sur des conneries que mobiliser sa connerie sur des choses intelligentes. »

      • [^] # Re: Obligatory XKCD

        Posté par  . Évalué à 3.

        Salut :)

        Voilà pourquoi tu te fait inutiler, il n'est pas sourd, il peut hocher/tourner la tête !

        Si tu savais comme c'est grave de se faire inutiler…

        Mais sais-tu que dans certaines cultures hocher de la tête veut dire non ?

        Oui ou non ?

        Matricule 23415

        • [^] # Re: Obligatory XKCD

          Posté par  . Évalué à 5.

          Ma femme et moi avons mis un peu de temps à comprendre que l'hôtesse d'accueil de notre hôtel à Bangalore ne se foutait pas de notre gueule en disant "ok" mais secouant la tête comme pour dire non… The Indian Head Bobble : https://www.youtube.com/watch?v=x96L18QBxSw

          M'enfin on peut raisonnablement penser que dans son grotte escape, l'individu muet partageait les mêmes codes culturels que les participants, + il y a bien d'autres façons de pouvoir signifier oui ou non ( ex 👍 )

  • # 2 essais, 1 erreur

    Posté par  (site web personnel) . Évalué à 5.

    Quand on arrive à la fin avec 2 réponses possibles, autant essayer directement, puisqu'on a droit à une erreur.

    Pourquoi bloquer la publicité et les traqueurs : https://greboca.com/Pourquoi-bloquer-la-publicite-et-les-traqueurs.html

    • [^] # Re: 2 essais, 1 erreur

      Posté par  . Évalué à 6.

      puisqu'on a droit à une erreur

      Pas d'erreur possible : « nous ne disposions que d'un essai »

  • # Essai

    Posté par  (site web personnel) . Évalué à 6.

    Dichotomie entre 000 et 999

    • q1: 500
    • q2: 250
    • q3: 125
    • q4: 62 vs 63
    • q5: 31 ou 32
    • q6: 15 ou 16
    • q7: 7 ou 8
    • q8: 3 ou 4
    • q9: 1 ou 2

    Si le bonus est atteignable, alors il faut 1 après q9, 3 après q8, 7 après q7, 15 après q6, 31 après q5. Il faut éviter les groupes de 32, donc éviter les groupes de 63. Donc la question 4 est le moment où tu commences à risquer le bonus, avec une chance sur deux.
    En gros une chance sur deux d'avoir le bonus par dichotomie, et sinon ensuite on peut être yolo et tenter une des deux possibilités restantes au pif, ou reposer une question 10 pour trancher avec certitude et sans bonus.

  • # est-ce que toi le muet qui (dés)opine tu connais le code ?

    Posté par  (site web personnel) . Évalué à 7. Dernière modification le 24 mars 2019 à 11:37.

    • non
    • ah…

  • # Par curiosité,

    Posté par  (site web personnel) . Évalué à 1.

    C'était une escape cave de David du GSI ?

  • # Entropie de Shannon

    Posté par  . Évalué à 8.

    Le nombre de questions oui/non nécessaires pour déterminer une quantité aléatoire est donné par l'entropie de Shannon. Si \mu est une probabilité sur \Omega un ensemble fini alors

    Si le code a été choisi selon une loi uniforme, cela donne donc une entropie de Shannon de \log_2(1000) \approx 9.97.

    Par contre, il se peut que ce code n'ait pas été choisi selon une loi uniforme, mais nous ne sommes pas censés le savoir.

  • # Quantité d'informations

    Posté par  . Évalué à 2. Dernière modification le 25 mars 2019 à 09:46.

    J'attaque un truc que je n'ai pas vu depuis 20 ans.

    La quantité d'information dans un chiffre à 3 chiffres ( donc < à 1024 ) est de 10 bits.

    Trouvez ce chiffre, signifie donc qu'il faut mettre à un 1 ou un 0 sur chaque bits et donc qu'il faut poser 10 questions pour être certains de trouver le bon.

    La méthode pour trouver en 9 questions et de poser 8 questions sur ces bits et de choisir au pif un nombre parmis les 4 restants pour le 9ième question.

    On peut s'arranger pour que les 8 bits posés permette d'inclure les chiffres entre 1000 et 1023 permettant de réduire le choix des nombres restants.

    • [^] # Re: Quantité d'informations

      Posté par  (site web personnel) . Évalué à 4.

      La quantité d'information dans un chiffre nombre à 3 chiffres (donc < 1024 1000) est de 10 bits.

      de rien :-)

      • [^] # Re: Quantité d'informations

        Posté par  . Évalué à 1.

        Ok pour chiffre.

        Non. C'est bien 1024 comme étant 210.

        • [^] # Re: Quantité d'informations

          Posté par  (site web personnel) . Évalué à 2.

          Non. C'est bien 1024 comme étant 210

          cela fait 24 nombres ayant plus de 3 chiffres (de 1000 à 1023…), qui ne feront pas partie de la solution demandée dans l'énoncée.

          • [^] # Re: Quantité d'informations

            Posté par  . Évalué à 3.

            D'où le dernier paragraphe de mon commentaire.

            Si le code a été choisi selon une loi uniforme, cela donne donc une entropie de Shannon de \log_2(1000) \approx 9.97.

            Après j'ai essayé de poser 9,97 questions. J'ai jamais réussi.

            • [^] # Re: Quantité d'informations

              Posté par  (site web personnel) . Évalué à 4.

              Suffit d'omettre le signe ? dans la phrase et c'est bon.

            • [^] # Re: Quantité d'informations

              Posté par  (site web personnel) . Évalué à 2. Dernière modification le 25 mars 2019 à 20:38.

              D'où le dernier paragraphe de mon commentaire.

              ah non, ça c'était le précédent commentaire

              Après j'ai essayé de poser 9,97 questions. J'ai jamais réussi.

              l'ensemble des français réussit à faire 1,18 % enfant en 2015 même si les chiffres sont présentés en / 1000 sans doute histoire de tromper son monde ? (ou la moyenne pour 10 femmes^W couples hétérosexuels ?!)

              ça veut dire que chaque enfant français est 18% plus qu'un autre enfant ? bah non, tu arrondis à 1 :-)

              Après j'ai essayé de poser 9,97 questions. J'ai jamais réussi.

              faut arrondir en enlevant les chiffres après la virgule, ce qui répond peut-être à l'escape grotte initial ? (c'est un choix d'arrondi !?)

  • # Solution en une question

    Posté par  (site web personnel) . Évalué à 9.

    Tu composes le code ou on te pète les dents?

    Le post ci-dessus est une grosse connerie, ne le lisez pas sérieusement.

Suivre le flux des commentaires

Note : les commentaires appartiennent à celles et ceux qui les ont postés. Nous n’en sommes pas responsables.